원자
작성일 : 2023년 07월 02일 (Sunday)
Table of contents
고전 (보어모형)
원자는 원자핵과 전자로 이루어져 있다. 원자를 설명할 때는 제일 먼저 아래와 같은 고전적인 형태인 보어 원자모형을 시작으로 한다.
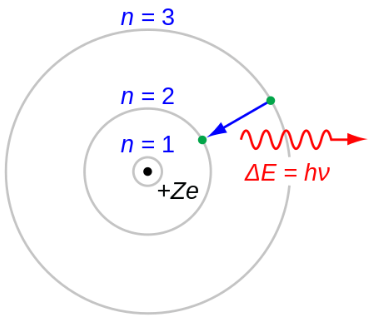

보어의 원자모형은 원자란 무엇인지 간단하게 살펴보기에는 좋지만, 현대과학과 맞지 않는 부분이 많다. (각 주기 별 전자의 에너지를 계산하는 부분은 현대의 양자 모형과 다르지 않다.)
현대 (양자모형)
과거 전자를 단순 입자라고 여겼지만, 현대에 와서는 드브로이, 슈뢰딩거, 하이젠베르크에 의해 전자가 입자성을 띄고 있으면서 파동성도 띄고 있다는 파동역학의 개념이 적용되었다.
물질파(드브로이파) 이론
전자가 파동과 입자의 성질을 모두 지니고 있다는 이론이다. 아래는 물질파 이론의 핵심인 드브로이 방정식이다. $\lambda$는 파장, h는 플랑크 상수, p는 운동량, E는 에너지, $\overline{h}$는 h-bar(혹은 디랙 상수. $\frac{h}{2\pi}$), k는 파수($k = \frac{2\pi}{\lambda}$), w는 각진동수이다.
$$ \lambda = \frac{h}{p} \tag{1} $$
$$ f = \frac{E}{h} \tag{2} $$
$$ p = \overline{h}k \tag{3} $$
$$ E = \overline{h}w \tag{4} $$
드브로이 방정식
$h = 6.6267015 \times 10^{-34} \mathrm {J\cdot s}$
하이젠베르크의 불확정성의 원리
하이젠베르크에 의하면 원자에서 전자가 어디에 존재하는 지 정확히 아는 것은 불가능하다. 아래 식과 같이 입자의 운동량을 정확히 알게되면, 위치가 불확실해지고, 위치를 정확히 알려고 하면 운동량을 알 수가 없다는 것이다. 따라서 전자가 정해진 궤도를 따라 핵 주위를 돈다는 보어의 가설은 틀린 것이다.
$$ \Delta{x}\Delta{mv} \geq (\frac{h}{4\pi}) $$
불확정성의 원리
슈뢰딩거의 방정식 은 물질을 구성하는 입자 또는 파동의 위치 상태를 확률적으로 표현한 함수이다. 하이젠베르크의 불확정성의 원리와 관점이 다르지만 역시 양자의 불연속성을 설명해 냈다.
오비탈
오비탈은 보어모형에서 다루는 궤도와는 다른말이다. 오비탈은 ‘궤도스러운’이라는 뜻인데 즉 궤도는 아니지만, 궤도처럼 규칙이 있음을 의미한다. 오비탈은 원자가 존재할 수 있는 공간을 나타내는 것으로 s, p, d, f 오비탈의 형태가 각각 다르다.
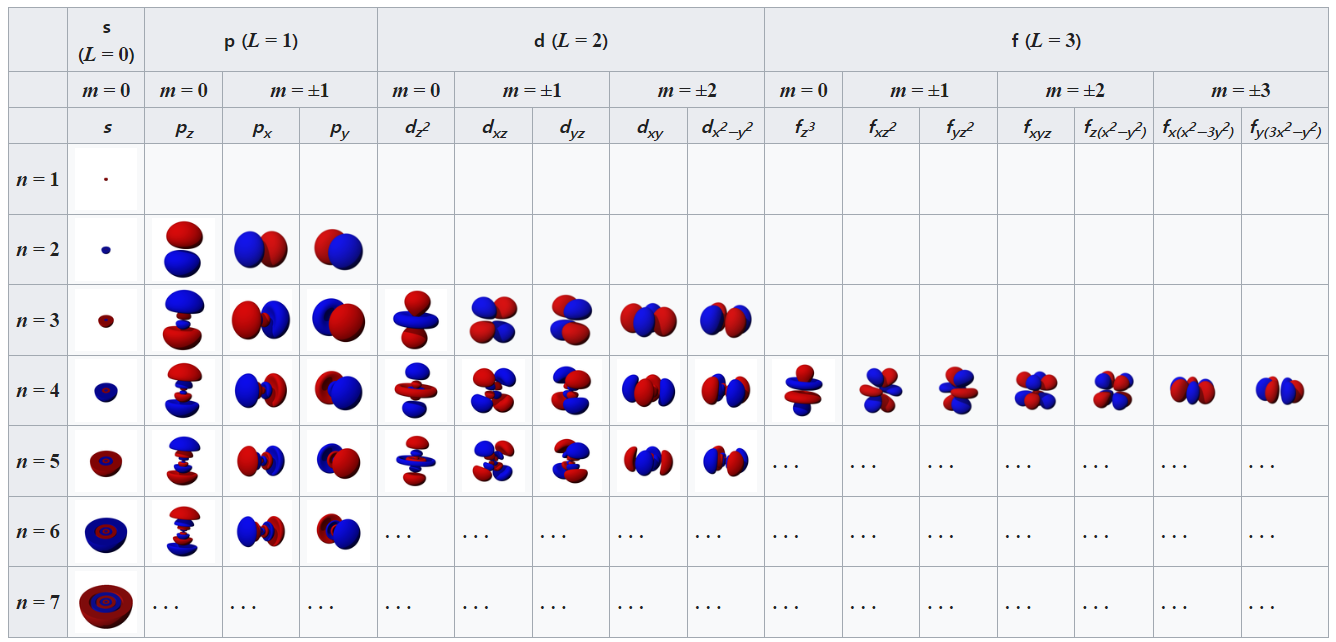

</figure>
–>