선형대수학 학습 의의
작성일 : 2023년 01월 28일 (Saturday)
선형대수학은 대수방정식이 선형일 때 사용할 수 있다. 함수가 선형인지 아닌지는 아래와 같이 변수의 차수가 모두 정수배이고, 방정식안에 변수가 모두 독립적으로 정의가 되어 있는지를 보면 된다. 아래와 같이 변수 2개($x_1$, $x_2$)의 곱이 포함되거나 변수의 차수가 정수배가 아닌 경우($\frac{1}{2}$) 비선형이라고 정의한다.
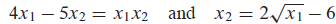
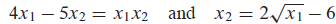
행렬 표현법 (Matrix Notation)
선형대수학은 행렬 표현법으로 함수를 표현한다. 행렬 표현법은 방정식의 계수를 행렬로 표현하는 것으로 복잡하지 않다. 아래의 예시를 보면 곧바로 이해할 수 있다. 선형 함수의 좌변의 계수만 따서 만든 행렬은 계수행렬, 함수의 우변까지 포함하는 행렬을 첨가행렬이라고 부른다. 세로는 행, 가로는 열로 표한하고 아래의 계수행렬은 3행3열(3x3) 행렬이고, 첨가행렬은 3행4열(3x4) 행렬이다.
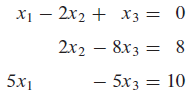
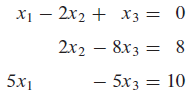
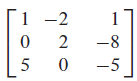
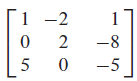
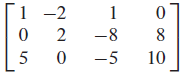
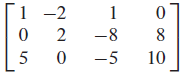
위 행렬을 이용해서 방정식을 풀어내는 과정은 연립방정식을 풀이하는 과정과 다르지 않다.
사다리꼴 행렬 (Echelon Matrix; StepLike Matrix)
사다리꼴 행렬은 아래와 같이 계단처럼 다음 행의 시작점이 이전 행의 시작점보다 오른쪽에 있는 행렬을 말한다. 모든 행의 시작점이 1이 되도록 정리하는 것이 기약 사다리꼴 행렬 (Row Reduced Echelon Form) 이다.
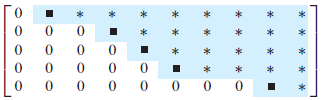



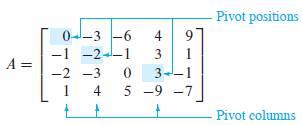

위와 같이 기약 사다리꼴 행렬에서 각 행의 첫번째 시작점을 추축점(Pivot Position), 추축점이 위치한 열을 추축열(Pivot Columns)라고 한다. 추축점에 위치한 변수를 기본 변수, 추축열에 포함되지 않은 변수를 자유 변수 라고 한다.