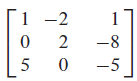고유벡터와 고유값

작성일 : 2023년 02월 05일 (Sunday)

Table of contents

1. 정의
2. 계산방법 예시
3. 특성방정식
4. 유사도(Similarity)와 유사변환

정의

고유벡터는 $A\textbf{x} = \lambda\textbf{x}$를 만족시키는 영 벡터가 아닌 $\textbf{x}$를 말한다. 여기서 $\lambda$는 스칼라 값으로 고유값으로 정의된다.

계산방법 예시

A가 위와 같을 때, 고유값과 고유벡터를 구해보자

$A\textbf{x} = \lambda\textbf{x}$를 만족시키는 $\lambda$와 $\textbf{x}$를 구하기 위해서 아래와 같이 A에 항등행렬에 7을 곱한 행렬을 빼주면 아래와 같다.

$\begin{vmatrix} -6 \\ 5 \end{vmatrix}$, $\begin{vmatrix} 6 \\ -5 \end{vmatrix}$는 너무나도 명백하게 선형종속관계에 있으므로, 비자명해를 갖고 결과적으로 고유값은 7이고, 고유벡터는 $\begin{vmatrix} 1 \\ 1 \end{vmatrix}$이다.

특성방정식

행렬방정식의 곱셈 특성 5항에 따라 $A\textbf{x} = \lambda\textbf{x}$를 정리하면, $(A-{\lambda}I)\textbf{x} = \textbf{0}$이 된다. 고유벡터를 가지기 위해서는 $\textbf{x}$가 자명해가 아니어야 한다. 그렇기 위해서는 $A-{\lambda}I$이 역행렬을 가지면 안되므로 $A-{\lambda}I$의 행렬식이 0인 조건을 만족하도록 하는 고유값을 찾으면 된다. 이 때, det($A-{\lambda}I$)를 특성방정식(Charateristic Equation)이라고 한다.

유사도(Similarity)와 유사변환

위에서 언급했듯, 특성방정식은 고유벡터와 고유값을 찾을 때 사용된다. 하지만, 고차방정식으로 갈 수록 직접 해를 찾는 것은 당연히 어려워질 것이다. 이를 보완하기 위해 적용된 개념이 유사도이다. 만약, $P^{-1}AP = B$를 만족하는 $A$, $B$가 있다면 $A$와 $B$는 서로 유사하다고 볼 수 있다. 위와 같이 B를 A의 형태로 여러 행렬로 나누어서 표현하는 변환을 유사변환(Similarity Transformation)이라고 한다.

---

---