상태공간 방정식 라플라스 변환식
작성일 : 2025년 05월 28일 (Wednesday)
사실 이전 포스트에서 상태공간 방정식의 컨셉은 설명했지만, 실제로 어떻게 사용해야 하는지는 잘 와닿지 않았을 것이다. 상태공간 방정식을 라플라스 변환을 통해 s 변수로 표현해보고, n차 시스템에 대해서 사용해보며 상태공간 방정식의 장점을 살펴보자.
상태공간 방정식의 라플라스 형태
상태공간 방정식을 다시 봐보자. 일단 가장 간단한 형태인 1차 시스템에 대해서만 분석해보자.
$$ \dot{x}(t) = \mathsf{A}x(t) + \mathsf{B}u(t) \tag{1} $$
$$ y(t) = \mathsf{C}x(t) + \mathsf{D}u(t) \tag{2} $$
상태공간 방정식 (1)과 출력식 (2)
지금까지는 상태공간 방정식을 시간에 대해서만 나타냈었다. 이를 라플라스 형태로 변환해보자.
$$ sX(s) - x(0) = AX(s) + BU(s) $$
$$ Y(s) = CX(s) + DU(s) $$
상태공간 방정식의 라플라스 표현
A, B, C, D 행렬은 상수이므로 그대로 가져와지고 x(t), u(t), y(t) 는 X(s), U(s), Y(s) 로 쉽게 변환되었다. 그런데 전달함수란 시스템의 응답을 보는 것이므로 x(0)은 0이라고 설정할 수 있다. 따라서, 이를 X(s), Y(s) 에 정리하면 새로운 식을 얻는다.
$$ (sI - A)X(s) = BU(s) $$
$$ X(s) = (sI - A)^{-1}BU(s) $$
$$ Y(s) = CX(s) + DU(s) = C(sI - A)^{-1}BU(s) + DU(s) = \left [ C(sI - A)^{-1}B + D \right ]U(s) $$
$$ G(s) = \frac{Y(s)}{U(s)} = C(sI - A)^{-1}B + D \tag{1} $$
라플라스 변환으로 얻어진 전달함수
(1) 식은 $\frac{G(s)}{\left \vert sI - A \right \vert}$로도 표현할 수 있다. 따라서 G(s)의 특성 방정식은 $\left \vert sI - A \right \vert$ 이고, 이 특성방정식의 고유값이 G(s)의 극점이 된다. 이제 상태공간 방정식을 통해 입력과 출력에 대한 식을 구할 수 있고, 다입력/다출력 시스템을 계산할 수 있게 되었다.
n차 시스템의 상태공간 방정식
n차 시스템의 경우도 한번 고려해보자. n차 시스템은 다음과 같은 경우라고 생각할 수 있을 것이다. 사실 시간영역에서 정의된 n차 방정식의 해를 시간영역에서 구한다는 것은 감히 상상하기 어렵다. 따라서, 라플라스 변환을 통해 s 공간에서 해를 구해보려고 하는 것이 상태공간 방정식이다.
2가지의 케이스를 고려해보자. 입력이 단순히 상수인 경우와 입력조차 n차 시스템의 출력인 경우이다. 식으로 나타내면 다음과 같다.
$$ y^{n} + a_{1}y^{n-1} + \cdot \cdot \cdot + a_{n-1}y^{1} + a_{n}y = u \tag{1} $$
$$ y^{n} + a_{1}y^{n-1} + \cdot \cdot \cdot + a_{n-1}y^{1} + a_{n}y = b_{0}u^{n} + b_{1}u^{n-1} + \cdot \cdot \cdot + b_{n-1}u^{1} + b_{n}u \tag{2} $$
n차 시스템의 입출력 관계식 (2가지 케이스)
케이스 1 (CCF : Controallbe Canonical Form, 제어 가능 표준형)
위에서 설명한 식 (1)을 정리해보자. 이런 경우에는 $\dot{y}^{n-1}$을 $x_{n}$으로 두고, $\dot{x}{n-1}$ 은 $x{n}$ 과 같다고 설정해서 풀면 간단하게 정리된다.
$$ y^{n} + a_{1}y^{n-1} + \cdot \cdot \cdot + a_{n-1}y^{1} + a_{n}y = u $$
$$ \dot{x}^{n} + a_{1}\dot{x}^{n-1} + \cdot \cdot \cdot + a_{n-1}\dot{x}^{1} + a_{n}y\dot{x}_{0} = u $$
$$ \dot{x}^{n} = -a_{n}\dot{x}_{0} - a_{n-1}\dot{x}^{1} - \cdot \cdot \cdot - a_{1}\dot{x}^{n-1} + u $$
$$ \dot{x}^{n} = -a_{n}x_{1} - a_{n-1}x_{2} - \cdot \cdot \cdot - a_{1}x_{n} + u $$
$$ \dot{\mathsf{x}} = \mathsf{A}\mathsf{x} + \mathsf{B}u $$
$$ y = \mathsf{C}\mathsf{x} $$
CCF 형태의 n차 시스템의 상태공간 방정식 풀이
이 경우 A, B, C의 값은 다음과 같다. D는 0이다.
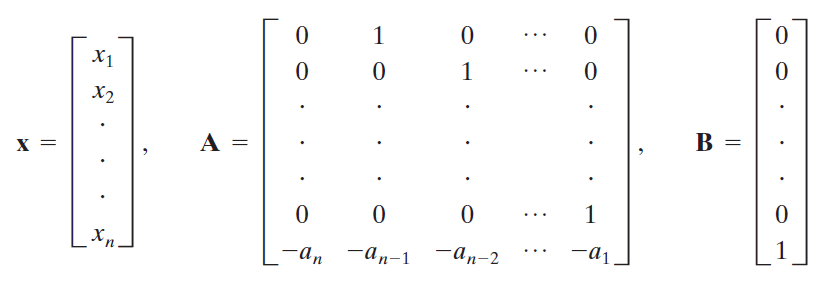
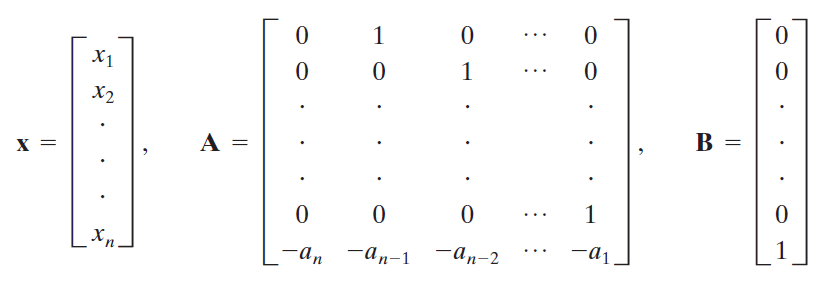
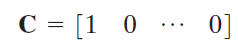
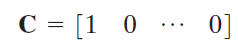
우리는 전달함수를 구하는 것으로 모든 y 및 y의 도함수에 대해 초기값을 0이라고 설정할 것이다. (사실 이는 노이즈 때문에 정확한 방법은 아니기는하다.) 이렇게 되면 전달함수는 다음과 같다.
$$ \frac{Y(s)}{U(s)} = \frac{1}{s^{n} + a_{1}s^{n-1} + \cdot \cdot \cdot + a_{n-1}s + a_{n}} $$
전달함수
예시
입력이 미래의 상태에 직적적으로 영향을 미치는 형태를 말한다. 가장 직관적인 예는 직선 운동하는 물체를 말한다. 가속도를 \(\dot{x}_{2}\), 속도를 \(\dot{x}_{1}\), 변위를 \(x_{1}\) 이라고 할 때, 물체 1kg에 가해진 힘이 1N이라고 하면, 다음과 같이 나타낼 수 있다. 힘은 u(t)로 나타낼 수 있다.
$$ \dot{\mathsf{x}} = \begin{bmatrix} \dot{x}_{1} \\ \dot{x}_{2} \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \end{bmatrix} u(t) $$
질량 1kg에 힘 u가 가해졌을 때의 직선운동을 나타낸 상태공간 방정식
케이스 2 : 입력이 n차 시스템의 출력인 경우
To Be Continued…
