정전계
작성일 : 2023년 12월 10일 (Sunday)
Table of contents
정전계는 동일한 관성계에서 멈춰있는 전하에 의한 전계를 말한다. 이번 포스트에서는 전하에 의한 전계, 전위의 크기를 구하는 방법에 대해 논한다.
쿨롱의 법칙
쿨롱의 법칙은 두 전하 간 작용하는 힘을 말한다. 쿨롱의 법칙은 같은 부호의 전기에 대해서는 척력이, 반대 부호의 전기에 대해서는 인력이 존재한다. 쿨롱의 법칙은 만유인력의 법칙의 공식과 거의 유사하다.
$$ F = \frac{Q_1Q_2}{4\pi \epsilon _0 r^2}\overrightarrow{e_r} = 9 \times 10^9 \times \frac{Q_1Q_2}{r^2} \boldsymbol{\widehat{\xi}} $$
쿨롱의 법칙
위에서 $\epsilon$은 진공의 유전율로 $8.85 \times 10^{-12}\frac{C^2}{N\cdot m^2}$이고, $\epsilon _r$는 상대유전율이다.
전계 (Electric Field)
전계란 특정 위치에 위치한 단위 정전하 1C에 대해 가해지는 벡터장을 의미한다. 전계의 세기는 N/C 혹은 V/m를 사용한다.
$$ E = \frac{1}{4\pi \epsilon _0}\sum_{i = 1}^{n}\frac{q_i}{r^2_i} \boldsymbol{\widehat{\xi}} $$
전계
$$ E(r)_{general} = \frac{1}{4\pi \epsilon _0}\int \frac{1}{\xi^2} \boldsymbol{\widehat{\xi}}dq $$
$$ E(r)_{line} = \frac{1}{4\pi \epsilon _0}\int \frac{\lambda (r)}{\xi^2} \boldsymbol{\widehat{\xi}}dl $$
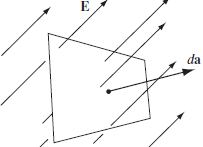
$$ E(r)_{surface} = \frac{1}{4\pi \epsilon _0}\int \frac{\sigma (r)}{\xi^2} \boldsymbol{\widehat{\xi}}da $$
$$ E(r)_{volume} = \frac{1}{4\pi \epsilon _0}\int \frac{\rho (r)}{\xi^2} \boldsymbol{\widehat{\xi}}d\tau $$
전하 분포 별 전계 (선점하, 면점하, 체적전하)
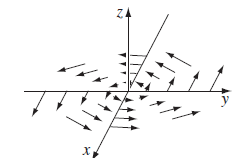
전계는 전기력선이 얼마나 촘촘한지로도 가늠할 수 있다.
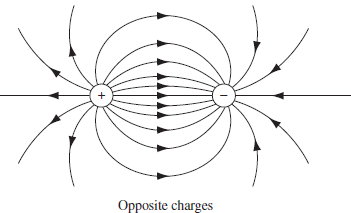

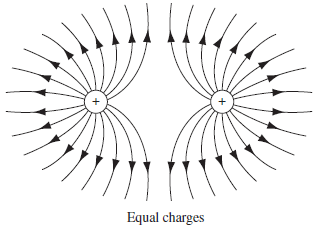

가우스의 법칙 (맥스웰 제 1법칙)
가우스는 폐곡면에서 발산하는 전기력선의 합은 $\nabla \cdot E$은 $\frac{\rho}{\epsilon}$이라는 내용이다. 이 공식을 이용해서 특정위치에서 전계의 세기를 구할 수 있다.
예제
- 점 전하 Q와 거리가 r만큼 떨어진 곳에서의 전계
구의 표면적을 구해서 $E \times S = \frac{Q}{\epsilon _0}$ 에 대입하면 전계가 얻어진다. $S = 4\pi r^2$이므로 $E = \frac{Q}{4\pi \epsilon _0 r^2}$이다. - 선 전하 Q와 거리가 r만큼 떨어진 곳에서의 전계 선 전하 밀도에 대해서는 원통으로 표면을 잡아서 구하면 된다. $S = 2\pi rl$ 이므로 $E = \frac{Q}{2\pi \epsilon _0 rl}$이다.
전계의 발산과 회전
일반적으로 전계의 발산은 가우스의 법칙, 전계의 회전은 암페어 주회 법칙과 연관된다. (맥스웰 법칙을 참고하자.)
하지만, 정전계에서 자계와의 연관성은 고려하지 않고 발산만한다고 가정하기 때문에 $\nabla \times E = 0$ (스토크 정리;Stoke’s theorem)이다.
전위 (Electric Potential)
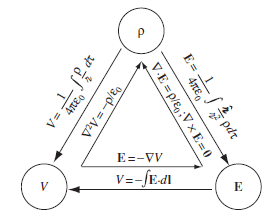
전위란 전계에 위치한 전하의 (위치) 에너지를 말한다. 전계에서 전하가 위치한 곳에 따라 포텐셜(위치 에너지)가 다르다. 뉴턴의 운동법칙이 전자기학에서도 통하므로 $F = qE = ma$이 된다. 전하량을 q라고 하면 가속도는 E가 된다. 그런데, 실은 전기는 전자의 이동에 의한 것이므로 전자의 입장에서는 전기장의 반대방향으로 힘을 받는다고 볼 수 있다. 아래 공식에 경도 정리 식인 $dT = (\nabla T) \cdot (dl)$ 를 적용하면, $E = -\nabla V$가 얻어진다.
$$ V(b) - V(a) = -\int_{O}^{b} E \cdot \,dl + \int_{O}^{a} E \cdot \,dl = - \int_{a}^{b} E \cdot \,dl $$
$$ dV = V(b) - V(a) = \int_{a}^{b} (\nabla V) \cdot \,dl $$
$$ \therefore E = - \nabla V $$
전위 공식
전위를 얻는 방법은 다음과 같다.
$$ V(r) - V(\infty) = V(r) = -\int_{\infty}^{r} E \cdot \,dl = \frac{-1}{4\pi \epsilon _0}\int_{\infty}^{r}\frac{q}{r^2}dr = \frac{1}{4\pi \epsilon _0}\frac{q}{r} $$
전위
전속밀도 D
전속밀도로 전속이 얼마나 많이 형성됐는 지를 알 수 있다. 전기력선은 전기장에 의해 분극된 전자 당 1개씩 생성되고, 전속은 전기력선의 합이므로, 전속밀도란 단위 부피당 전속을 말한다.
$$ \overrightarrow{D} = {\epsilon}_0\overrightarrow{E} + {\chi}_0{\epsilon}_0\overrightarrow{E} = {\epsilon}_0(1 + {\chi}_0)\overrightarrow{E} = {\epsilon}_0{\epsilon}_r\overrightarrow{E} = {\epsilon}\overrightarrow{E} $$
전속밀도 식
푸아송/라플라스 방정식
위 전위 식과 가우스의 법칙을 결합하면 푸아송 방정식의 형태가 얻어진다. 푸아송 방정식($\nabla ^2 \Phi = \sigma (x)$)은 이전글에서 다뤘듯이 선속과 소스와의 관계를 가리킨다. 일단, 아래의 식을 보자.
$$ \nabla \cdot E = \frac{\rho}{\epsilon _0} $$
$$ =- \nabla \cdot \nabla V $$
$$ \therefore \nabla ^2 V = -\frac{\rho}{\epsilon _0} $$
전위와 관련된 푸아송 방정식
푸아송 방정식이 선속과 소스의 관계를 나타낸 식이므로 다시 정리해보자면, 라플라스 방정식은 내부 전하가 없는 경우에 대해서 다룬 것이다.
결론
결론적으로 다음과 같이 정리된다.