필터 (아날로그)
작성일 : 2025년 04월 06일 (Sunday)
Table of contents
회로 설계시에는 특정 IC나 직접설계한 회로 등 간에 신호를 주고받을 때 잘못된 값으로 잘못 해석되지 않도록 시그널 컨디셔닝 작업을 한다. 시그널 컨디셔닝 작업은 신호를 조금 더 알아먹기 좋은 상태로 처리해주는 작업인데, 예를 들어 LOW를 0V~1V 사이값으로, HIGH를 4V~5V로 인식하는 칩이 있을 때, 특정 회로에서 로직 상 LOW를 출력했는데 회로를 거쳐가다 보니 받는 쪽에서 플로팅 상태로 인식할 가능성이 있을 때 시그널 컨디셔닝이 필요할 수 있다. 그 원인은 공통 모드 노이즈, EMI 간섭 등 다양한데, 용도에 따라 형태는 다양하지만 이 때마다 보통 필터를 적용해서 해결한다.
그렇다면 필터의 역할은 무엇일까?
필터는 무엇을 개선하는 것일지 필터의 본질부터 살펴볼 필요가 있다. 브리타같은 정수필터를 생각해보자. 브리타는 사람이 마실 수 있는 정도로 석회질이나 중금속들을 걸러준다. 해수를 담수화시켜주는 필터도 존재한다. 그러면 회로 입장에서 석회질이나 중금속에 해당하는 것은 무엇일까? 그 답은 회로 나름이라는 것이다. DC 를 입력으로 하는 곳은 DC 가 아닌 성분들이 걸러줘야 하는 성분이 되고, 차동증폭기를 이용한 센서 회로처럼 차동 입력을 받는 곳에서는 공통모드 노이즈가 문제가 된다. 만능필터는 없다. 용도에 맞는 필터를 적재적소에 필요한 정도로만 사용해야 회로도 탈이 나지 않고 정상작동할 수 있다. 필터의 종류를 하나하나 살펴보자.
필터의 분류
흔히 회로에서 필터라고 하면 수동필터를 많이 사용한다. 본인은, 필터하면 가장 먼저 떠오르는 것이 RC 필터(LPF) 나 Y-CAP 정도가 떠오른다. 전력 전자 회로를 담당하시는 분들은 아무래도 공통 모드 노이즈나 서지 등이 골치아픈 주제이기도 하니 DC 쵸크나 X-CAP 을 먼저 떠올릴 지도 모르겠다. 능동필터도 꽤 많이들 사용한다. 특히 시그널 컨디셔닝이다 하면 능동필터를 사용한다. 이유는 수동필터는 신호가 감쇄되기만 해서 이득이 1을 넘지 못하기 때문이다.
주파수 필터
주파수에 따라서 어느 범위의 주파수는 통과시키고, 어느 범위의 주파수는 차단하는 필터를 주파수 필터라고 한다. 주파수 필터는 대표적으로 LPF, HPF, BPF, BSF(Notch Filter)가 있다. LPF는 Low Pass Filter로 저주파를 통과시키고, HPF는 High Pass Filter로 고주파를 통과시키고, BPF는 Band Pass Filter로 특정 범위의 주파수를 통과시키고, BSF는 Band Stop Filter(흔히 Notch Filter로 불림)로 특정 범위의 주파수를 차단한다. 구현방법은 다양한데 각 필터 별 대표적으로 한두가지 씩만 보고 넘어가도록 하자.
LPF (Low-Pass Filter)
LPF는 아래와 같이 설계할 수 있다. LPF는 저역주파수의 신호 정상적으로 통과시키고 고역주파수 신호는 감쇠시킨다.
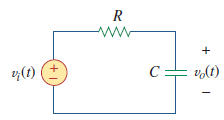

위 식을 보면, $w = \frac{1}{RC}$ 일 때 0.707배가 되는 것을 확인할 수 있다. 페이저의 위상을 보면, 저항에 대비해서 커패시터에 걸리는 전압은 $\phi$만큼 뒤지고, 전압은 전류에 비해서 $\frac{\pi}{2}$만큼 앞선다는 것을 알 수 있다.
HPF (High-Pass Filter)
HPF는 아래와 같이 설계할 수 있다. HPF는 고역주파수의 신호 정상적으로 통과시키고 저역주파수 신호는 감쇠시킨다.
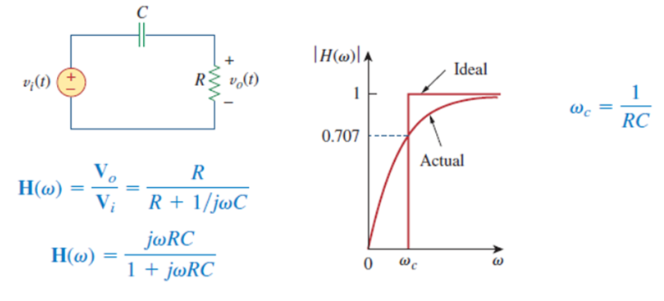

BPF (Band Pass Filter)
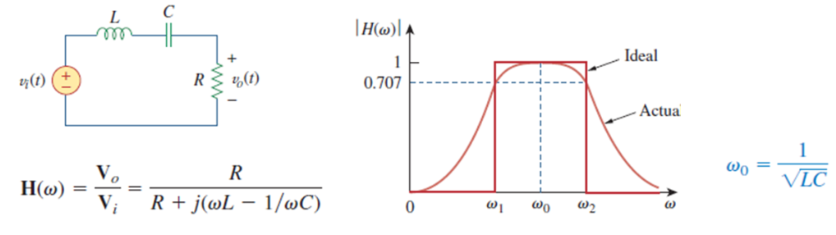

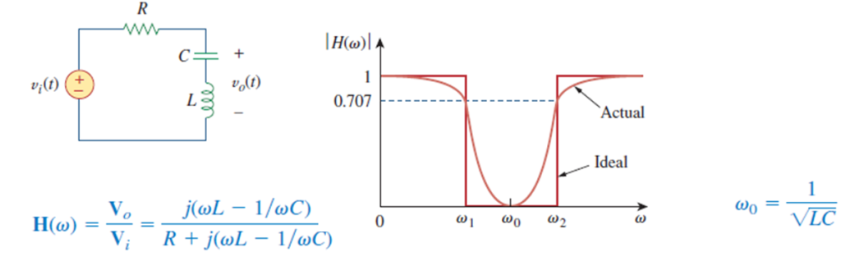
BSF (Band Stop Filter, Notch Filter)