벅부스트 컨버터

작성일 : 2023년 09월 18일 (Monday)

Table of contents

개요

이번 포스트에서는 승압, 강압이 가능한 비절연형 컨버터인 벅부스트 컨버터를 다룬다. 이번 포스트에서도 마찬가지로 아래의 룰이 적용된다.

컨버터 기본 설계 Rule (인덕터 에너지 저장형)
R1. 인덕터에 흐르는 전류와 저항에 흐르는 전류와 크기가 같고, 연속적이다. 다른 말로 한 주기동안 인덕터에 걸리는 전압의 평균은 0이다.
R2. 커패시터에 걸린 전압과 저항에 걸린 전압과 크기가 같고, 연속적이다. 다른 말로 한 주기동안 커패시터로 인해 발생한 전하량의 평균은 0이다.
R3. 부하는 가변적이다. 즉, 부하는 고정값이 아니므로 최대값, 최소값을 고려하여 컨버터를 설계해야 한다. 하지만, 한 주기내에서 부하는 일정하다고 가정한다.
R4. 컨버터는 전원공급장치로 출력전압이 항상 정상범위 이내를 유지할 수 있도록 인덕터에는 적당한 에너지가 유지되어야 한다.
R5. MOSFET 게이트 드라이버의 스위칭 주파수가 높을 수록 컨버터를 더욱 컴팩트하게 설계할 수 있다. 하지만, 스위칭 주파수가 높다는 말은 게이트 드라이버가 고가라는 말이기도 하다.
R6. 인덕터 전류는 매 주기마다 일정한 값을 가진다. 이는 부하가 고정이라는 가정에 의한 것으로 실제로는 조금 차이가 날 수 있지만 주기가 매우 짧으므로 그 차이는 사실 미미(무시가능한 수준)하다. 즉, 도통 때 증가한 전류량과 차단 때 감소한 전류량은 거의 동일하다. ($| i_L(t) | \simeq | i_L(t + T)$ |)
R7. 출력전압이 일정하게 유지되기 위해서 커패시터는 적당히 큰 값으로 설정해야 한다. 즉, 시정수 (RC)를 고려해서 스위치가 OFF 되어도 커패시터 충전량만으로도 한 주기 동안은 커버가 될 정도가 되어야 한다. 이 내용에 대한 사양은 보통 출력전압 리플 요구사양으로 제시된다.
R8. 인덕턴스가 시스템에서 요구하는 사양 대비 과도하게 커지지 않도록 최소 출력저항이 얼마인지 고려하는 단계가 필요하다.
R9. 경부하모드를 제외하고는 인덕터 전류는 항상 0보다 큰 값을 유지할 수 있도록 하는 인덕턴스 값을 갖는 인덕터를 사용해야 한다.

개요

벅부스트 컨버터의 형태는 다음과 같다. 벅부스트 컨버터의 원리는 승압형으로 사용할 때는 스위치 ON 시간을 늘려서 입력과 출력으로부터 동시에 에너지를 받아 인덕터에 저장되는 에너지를 크게 하고, 강압형으로 사용할 때는 스위치 OFF 시간을 늘려서 인덕터에 저장되는 에너지를 적게 함으로써 강압시킨다.

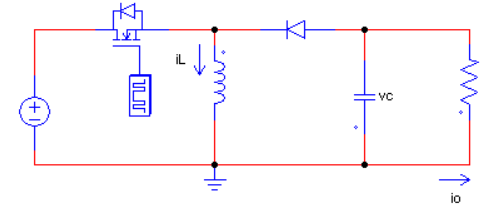
입출력 관계식은 위 Rule 6과 MOSFET OFF/SATURATION 시의 인덕터 전류를 비교하여 구할 수 있는데 과정은 다음과 같다.

$$ v_L = V_S = L\frac{di_L}{dt} $$

$$ \frac{di_L}{dt} = \frac{V_S}{L} $$

$$ (\Delta{i_L})_{closed} = \frac{V_SDT}{L} $$

한 주기 동안의 스위치 ON 때 인덕터 전류의 변화량

한 주기의 도통시간(스위치 ON 시간)은 주기에 시비율을 곱한 값으로 위에서 $dt$는 $DT$로 변환되었다.

$$ v_L = V_O = L\frac{di_L}{dt} $$

$$ \frac{di_L}{dt} = \frac{V_O}{L} $$

$$ (\Delta{i_L})_{open} = \frac{V_O}{L}(1-D)T $$

한 주기 동안의 스위치 OFF 때 인덕터 전류의 변화량

그런데 Rule 6에 의해서 한 주기 동안의 인덕터의 전류는 거의 동일하므로 아래와 같이 입출력 관계식을 얻을 수 있다.

$$ (\Delta{i_L})_{closed} \simeq (\Delta{i_L})_{open} $$

$$ \frac{V_SDT}{L} - \frac{V_O}{L}(1-D)T \simeq 0 $$

$$ V_O \simeq -V_S\frac{D}{1-D} $$

벅부스트 컨버터 입출력 관계식

위 식을 보면, 벅부스트의 출력전압은 입력전압과 반대라는 것을 알 수 있다.

아래에서 벅부스트 컨버터의 인덕터 전류가 연속이기 위한 인덕턴스를 계산해보자. 벅에서 계산했던 방식과 동일하게 $I_{max}$, $I_{min}$ 을 계산해서 $I_{min}$이 0보다 크도록 하는 인덕턴스의 최소값을 계산해내면 된다. $I_{max}$, $I_{min}$의 수식을 계산하기 위해서는 Rule 1 에 따라서, 인덕터 전류와 저항에 걸리는 전류가 동일함을 이용하여 계산하면 된다.

입력전류는 스위치가 ON일 때만 동작하므로, 입력전류의 평균값은 인덕터의 전류에 $\frac{t_{ON}}{t_{ON} + t_{OFF}}$ 이므로 $I_S = I_LD$가 된다. 이를 아래 (1)식에 대입하면 (2)식이 얻어진다. 그리고 (2)식을 $I_L$에 대해 정리하고, 입출력관계식을 대입하면 최종적으로 (3)식이 계산된다.

$$ P_i = P_o $$

$$ V_SI_S = V_OI_O = \frac{V^2_O}{R} \tag{1} $$

$$ V_SI_LD = \frac{V^2_O}{R} \tag{2} $$

$$ \therefore I_L = \frac{V^2_O}{V_SRD} = \frac{V_SD}{(1-D)^2R} \tag{3} $$

$$ I_{max} = I_L + \frac{\Delta i_L}{2} = \frac{V_SD}{(1-D)^2R} + \frac{V_SDT}{2L} $$

$$ I_{min} = I_L - \frac{\Delta i_L}{2} = \frac{V_SD}{(1-D)^2R} - \frac{V_SDT}{2L} $$

$$ \therefore L_{min} = \frac{(1-D)^2R}{2f} $$

벅부스트 컨버터 인덕터 최대·최소 전류

안정적인 전원공급을 위한 커패시터의 최소 커패시턴스를 계산하는 방법은 다음과 같다. 벅 컨버터와 마찬가지로 시스템에서 요구하는 출력전압의 리플을 적용하면 최소 커패시턴스를 계산할 수 있다.

$$ \Delta V_O = \frac{|\Delta Q|}{C} $$

$$ C = |\Delta Q|\frac{1}{\Delta V_O} $$

$$ C = \frac{V_ODT}{R}\frac{1}{\Delta V_O} $$