곡면좌표계
작성일 : 2024년 02월 02일 (Friday)
Table of contents
여러가지 형태에 대해서 전위와 전계를 계산하기 위해서는 가장 중요한 것은 어떤 좌표계를 사용해서 효과적으로 계산해내는지에 달렸다. 일반적으로 3차원 좌표계를 표현할 때 직교좌표계를 많이 사용한다. 하지만, 구형태의 전하로부터 r만큼 떨어진 곳의 전위, 전계를 계산할 때 직교좌표계를 사용하면 계산이 매우 복잡해진다. 따라서, 경우에 따라서는 원통좌표계, 어떤 경우에는 구면좌표계를 사용해야 쉽게 계산이 가능할 것이다.
좌표계의 종류와 변환
위에 설명했듯 좌표계는 직교좌표계, 원통좌표계, 구면좌표계가 존재한다. 각 좌표계에서 미소길이요소 $d\boldsymbol{l}$, 미소면적요소 $da$, 미소체적요소 d$\tau$를 표현하는 법과 좌표계에 대해서 경도, 발산, 회전, 라플라시안 계산법만 익히면 충분하다. 미소길이요소, 미소면적요소는 벡터량이고 미소체적요소는 스칼라량이다.
직각좌표계는 기저벡터로써 $\boldsymbol{\hat{x}}$, $\boldsymbol{\hat{y}}$, $\boldsymbol{\hat{z}}$를 사용하고, 원통좌표계는 $\boldsymbol{\hat{s}}$, $\boldsymbol{\hat{\phi}}$, $\boldsymbol{\hat{z}}$, 구면좌표계는 $\boldsymbol{\hat{r}}$, $\boldsymbol{\hat{\theta}}$, $\boldsymbol{\hat{\phi}}$를 사용한다. 기저벡터는 공간을 정의하기 위해 필요한 최소한의 벡터의 조합이다.
$d\boldsymbol{l}$, $d\boldsymbol{a}$, $d\tau$
아래는 직교좌표계 기준으로 미소길이요소 $d\boldsymbol{l}$, 미소면적요소 $da$, 미소체적요소 d$\tau$를 표현했다. 주의할 점은 계산을 하는 방향에 따라 특정 방향의 벡터는 무시해도 된다는 것이다.
$$ d\boldsymbol{l} = dx\boldsymbol{\hat{x}} + dy\boldsymbol{\hat{y}} + dz\boldsymbol{\hat{z}} $$
$$ d\boldsymbol{a_x} = d\boldsymbol{l}_yd\boldsymbol{l}_z\boldsymbol{\hat{x}} = dydz\boldsymbol{\hat{x}} $$
$$ d\boldsymbol{a_y} = d\boldsymbol{l}_xd\boldsymbol{l}_z\boldsymbol{\hat{y}} = dxdz\boldsymbol{\hat{y}} $$
$$ d\boldsymbol{a_z} = d\boldsymbol{l}_xd\boldsymbol{l}_y\boldsymbol{\hat{z}} = dxdy\boldsymbol{\hat{z}} $$
$$ d\tau = dxdydz $$
직교좌표계 기준 dl, da, dτ
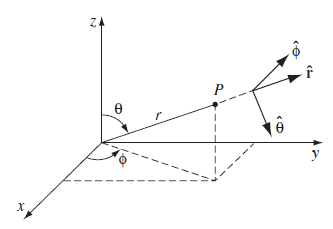



구면좌표계에서 $\theta$, $\phi$는 각각 극각(polar angle), 방위각(azimuthal angle)을 말한다. $\boldsymbol{\hat{r}}$ 벡터와 z축이 이루는 각도를 말한다. 방위각은 $\boldsymbol{\hat{r}}$ 벡터가 기존의 x축과 이루는 각도를 말한다.
위 그림 1.38을 보면 \(d\boldsymbol{l}_{r}\) , \(d\boldsymbol{l}_{\theta}\) , \(d \boldsymbol{l}_{\phi}\) 가 어떻게 변환되는지 알 수 있다.
\(d\boldsymbol{l}_{r}\)은 \(dr\boldsymbol{\hat{r}}\)로 바로 구해지고, \(d\boldsymbol{l}_{\theta}\)은 반지름 r에 호의 길이 공식을 적용하면 \(rd\theta \boldsymbol{\hat{\theta}}\) 가 구해지고, \(d\boldsymbol{l}_{\phi}\) 은 마찬가지로 호의 길이를 구하는 공식을 적용하되 r대신 $rsin\theta$ 를 사용해서 \(rsin\theta d\phi \boldsymbol{\hat{\phi}}\) 가 된다. 정리하면 다음과 같다.
$$ d\boldsymbol{l} = dr\boldsymbol{\hat{r}} + rd\theta \boldsymbol{\hat{\theta}} + rsin\theta d\phi \boldsymbol{\hat{\phi}} $$
$$ d\boldsymbol{a_r} = d\boldsymbol{l}_{\theta}d\boldsymbol{l}_{\phi}\boldsymbol{\hat{r}} = r^2sin\theta d\theta d\phi \boldsymbol{\hat{r}} $$
$$ d\boldsymbol{a_{\theta}} = d\boldsymbol{l}_{r}d\boldsymbol{l}_{\phi}\boldsymbol{\hat{r}} = r^2sin\theta d\phi \boldsymbol{\hat{\theta}} $$
$$ d\boldsymbol{a_{\phi}} = d\boldsymbol{l}_{r}d\boldsymbol{l}_{\theta}\boldsymbol{\hat{r}} = r^2 d\theta \boldsymbol{\hat{\phi}} $$
$$ d\tau = r^2sin\theta drd\theta d\phi $$
구면좌표계 dl, da, dτ
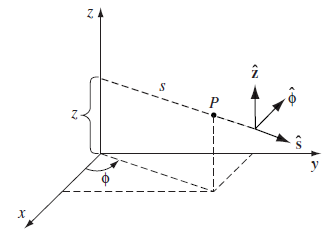

원통좌표계는 구면좌표계에서 극각이 없고 z를 사용한다. z는 직교좌표계의 z와 같다. 따라서 다음과 같이 표현된다.
$$ d\boldsymbol{l} = ds \boldsymbol{\hat{s}} + sd\phi \boldsymbol{\hat{\phi}} + dz \boldsymbol{\hat{z}} $$
$$ d\boldsymbol{a_{s}} = d\boldsymbol{l}_{\phi}d\boldsymbol{l}_{z}\boldsymbol{\hat{s}} = sd\phi dz\boldsymbol{\hat{s}} $$
$$ d\boldsymbol{a_{\phi}} = d\boldsymbol{l}_{s}d\boldsymbol{l}_{z}\boldsymbol{\hat{\phi}} = dsdz\boldsymbol{\hat{\phi}} $$
$$ d\boldsymbol{a_{z}} = d\boldsymbol{l}_{s}d\boldsymbol{l}_{\phi}\boldsymbol{\hat{z}} = sdsd\phi \boldsymbol{\hat{z}} $$
$$ d\tau = sdsd\phi dz $$
원통좌표계 dl, da, dτ
경도, 발산, 회전, 라플라시안
경도, 발산, 회전, 라플라시안 식을 아는 것도 중요하다. 구면좌표계와 원통좌표계에서의 경도, 발산, 회전, 라플라시안을 좌표계 별로 직접 구하는 방법이 꽤 복잡해서 일반화된 식을 통해 외워두는 것이 좋다. 아래에는 일반화된 공식을 얻는 과정을 적어놓았는데, 그 과정도 사실 만만치 않다. 정리된 공식만 외우는 것도 나쁘지 않은 선택같다. 다만, 발산의 정리, 스토크의 정리를 확실하게 알고 넘어가고자 한다면 유도과정을 이해해보고 따라해보는 것도 나쁘지만은 않다. (시간은 많이 걸린다.)
David은 직교좌표계와 곡면좌표계(구면좌표계, 원통좌표계)를 함께 표현하기 위해서 일반화된 u, v, w, f, g, h 변수를 사용했다.
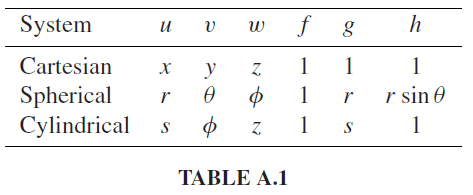

새로운 변수를 적용해서 $d\boldsymbol{l}$을 구해보면 다음과 같다.
$$ d\boldsymbol{l} = fdu\boldsymbol{\hat{u}} + gdv\boldsymbol{\hat{v}} + hdw\boldsymbol{\hat{w}} $$
곡면좌표계에서의 dl
경도
경도정리를 사용하면 경도 $\nabla{t}$는 다음과 같이 정리된다.
$$ dt = \frac{\partial t}{\partial u}du + \frac{\partial t}{\partial v}dv + \frac{\partial t}{\partial w}dw $$
$$ dt = \nabla{t} \cdot d\boldsymbol{l} = (\nabla{t})_{u}fdu + (\nabla{t})_{v}gdv + (\nabla{t})_{w}hdw $$
$$ d\boldsymbol{l} = fdu\boldsymbol{\hat{u}} + gdv\boldsymbol{\hat{v}} + hdw\boldsymbol{\hat{w}} $$
$$ \nabla{t} = \frac{1}{f}\frac{\partial t}{\partial u}\boldsymbol{\hat{u}} + \frac{1}{g}\frac{\partial t}{\partial v}\boldsymbol{\hat{v}} + \frac{1}{h}\frac{\partial t}{\partial w}\boldsymbol{\hat{w}} $$
각 좌표계에 대해서 구해보면 다음과 같다.
$$ \nabla{t}_{cartesian} = \frac{\partial t}{\partial x}\boldsymbol{\hat{x}} + \frac{\partial t}{\partial y}\boldsymbol{\hat{y}} + \frac{\partial t}{\partial z}\boldsymbol{\hat{z}} $$
직교좌표계에서의 경도
$$ \nabla{t}_{spherical} = \frac{\partial t}{\partial r}\boldsymbol{\hat{r}} + \frac{1}{r}\frac{\partial t}{\partial \theta}\boldsymbol{\hat{\theta}} + \frac{1}{rsin\theta}\frac{\partial t}{\partial \phi}\boldsymbol{\hat{\phi}} $$
구면좌표계에서의 경도
$$ \nabla{t}_{cylindrical} = \frac{\partial t}{\partial s}\boldsymbol{\hat{s}} + \frac{1}{s}\frac{\partial t}{\partial \phi}\boldsymbol{\hat{\phi}} + \frac{\partial t}{\partial z}\boldsymbol{\hat{z}} $$
원통좌표계에서의 경도
발산
어떤 벡터장 \(\overrightarrow{A}(u, v, w) = A_u\boldsymbol{\hat{u}} + A_v\boldsymbol{\hat{v}} + A_w\boldsymbol{\hat{w}}\) 가 존재한다고 할 때, 단위 체적에 대한 발산의 정리를 이용하면 일반화된 발산식이 얻어진다.
$$ \oint_S v \cdot da = \int_V (\nabla \cdot v) d\tau $$
$$ \oint_S v \cdot da = (\nabla \cdot v) d\tau $$
단위 체적에 대한 발산 정리
단위 체적에 대해서는 체적 적분을 할 필요가 없다. 그림 A.2에서 마주보고 있는 면에 대한 적분값의 크기는 거의 같고 부호는 반대이므로, 아래의 (1), (2), (3)을 더한 값이 전체 곡면에 대한 면적 적분 값이 된다. 이 내용만 이해하면 발산을 유도하는 과정을 이해할 수 있다.
$$ d\boldsymbol{l} = fdu\boldsymbol{\hat{u}} + gdv\boldsymbol{\hat{v}} + hdw\boldsymbol{\hat{w}} = dl_u\boldsymbol{\hat{u}} + dl_v\boldsymbol{\hat{v}} + dl_w\boldsymbol{\hat{w}} $$
$$ da_u = dl_v dl_w \boldsymbol{\hat{u}} = (gh)dvdw \boldsymbol{\hat{u}} $$
$$ da_v = dl_u dl_w \boldsymbol{\hat{v}} = (fh)dudw \boldsymbol{\hat{v}} $$
$$ da_w = dl_u dl_v \boldsymbol{\hat{w}} = (fg)dudv \boldsymbol{\hat{w}} $$
$$ F_u = A_u \cdot da_u $$
$$ F_v = A_v \cdot da_v $$
$$ F_w = A_w \cdot da_w $$
$$ \oint_S A \cdot da = \{F_u(u + du) - F_u(u)\} + \{F_v(v + dv) - F_v(v)\} + \{F_w(w + dw) - F_w(w)\} $$
$$ F_u(u + du) - F_u(u) = \frac{\partial F_u}{\partial u}du = \frac{\partial}{\partial u}(gh)A_ududvdw = \frac{1}{fgh}\frac{\partial}{\partial u}(ghA_u)d\tau \tag{1} $$
$$ F_v(v + dv) - F_v(v) = \frac{\partial F_v}{\partial v}dv = \frac{\partial}{\partial v}(fh)A_ududvdw = \frac{1}{fgh}\frac{\partial}{\partial v}(fhA_v)d\tau \tag{2} $$
$$ F_w(w + dw) - F_w(w) = \frac{\partial F_w}{\partial w}dw = \frac{\partial}{\partial w}(fg)A_ududvdw = \frac{1}{fgh}\frac{\partial}{\partial w}(fgA_w)d\tau \tag{3} $$
$$ (\because \frac{1}{fgh}d\tau = dudvdw) $$
$$ \oint_S A \cdot da = \frac{1}{fgh}[\frac{\partial}{\partial u}(ghA_u) + \frac{\partial}{\partial v}(fhA_v) + \frac{\partial}{\partial w}(fgA_w)]d\tau $$
$$ \nabla \cdot A = \frac{1}{fgh}[\frac{\partial}{\partial u}(ghA_u) + \frac{\partial}{\partial v}(fhA_v) + \frac{\partial}{\partial w}(fgA_w)]d\tau $$
단위 체적을 기준으로 일반화된 발산 공식 유도

$$ \nabla \cdot A = \frac{\partial A_x}{\partial x} + \frac{\partial A_y}{\partial y} + \frac{\partial A_z}{\partial z} $$
직교좌표계에서의 발산
$$ \nabla \cdot A = \frac{1}{r^2\sin{\theta}}\frac{\partial r^2\sin{\theta} A_r}{\partial r} + \frac{1}{r^2\sin{\theta}}\frac{\partial r\sin{\theta} A_{\theta}}{\partial \theta} + \frac{1}{r^2\sin{\theta}}\frac{\partial rA_{\phi}}{\partial \phi} $$
$$ = \frac{1}{r^2}\frac{\partial }{\partial r}(r^2 A_r) + \frac{1}{r\sin{\theta}}\frac{\partial }{\partial \theta}(\sin{\theta} A_{\theta}) + \frac{1}{r\sin{\theta}}\frac{\partial A_{\phi}}{\partial \phi} $$
구면좌표계에서의 발산
$$ \nabla \cdot A = \frac{1}{s}\frac{\partial s A_s}{\partial s} + \frac{1}{s}\frac{\partial A_{\phi}}{\partial \phi} + \frac{1}{s}\frac{\partial sA_z}{\partial z} $$
$$ = \frac{1}{s}\frac{\partial }{\partial s}(s A_s) + \frac{1}{s}\frac{\partial A_{\phi}}{\partial \phi} + \frac{\partial A_z}{\partial z} $$
원통좌표계에서의 발산
회전
발산과 마찬가지로 어떤 벡터장 \(\overrightarrow{A}(u, v, w) = A_u\boldsymbol{\hat{u}} + A_v\boldsymbol{\hat{v}} + A_w\boldsymbol{\hat{w}}\) 가 존재한다고 할 때, 단위 면적에 대해 스토크의 정리를 적용하면 회전 공식이 얻어진다.
$$ \oint_P v \cdot dl = \int_S (\nabla \times v) \cdot da $$
$$ \oint_P v \cdot dl = (\nabla \times v) \cdot da $$
단위 면적에 대한 스토크의 정리
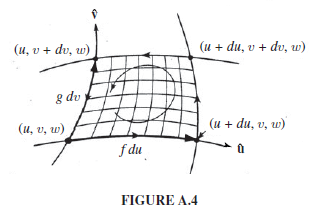

위 그림은 w 방향 평면에 대한 curl의 그림이다. (u + du, v, w) 점, (u, v + dv, w) 점에서 각각 \(\boldsymbol{\hat{u}}\), \(\boldsymbol{\hat{v}}\) 방향으로의 벡터를 모두 더하면, w 방향에 대한 회전이 구해진다. 곡면은 \(\boldsymbol{\hat{u}}\), \(\boldsymbol{\hat{v}}\), \(\boldsymbol{\hat{w}}\) 모든 방향에 대해 존재하므로 각각의 방향에 대해 구해서 더하면 벡터장 A에 의한 총 회전 \(\nabla \times A\)가 얻어진다.
공식을 유도하는 과정 자체가 복잡하고 여러 번 해본 결과, 위 설명 이외에 특별한 내용이 없이 복잡하기만 해서 결과만 남긴다. 추후 필요하다고 생각되면 추가하겠다.
$$ \nabla \times A = $$
$$ \frac{1}{gh}\left[\frac{\partial}{\partial v}(hA_w) - \frac{\partial}{\partial w}(gA_v)\right]\boldsymbol{\hat{u}} $$
$$ + \frac{1}{fh}\left[\frac{\partial}{\partial w}(fA_u) - \frac{\partial}{\partial u}(hA_w)\right]\boldsymbol{\hat{v}} $$
$$ + \frac{1}{fg}\left[\frac{\partial}{\partial u}(gA_v) - \frac{\partial}{\partial v}(fA_u)\right]\boldsymbol{\hat{w}} $$
단위 면적을 기준으로 일반화된 회전 공식 유도
위 식이 복잡해서 외우기가 여간 쉽지 않다. 1번 포스트에서 다뤘던 것처럼 매트릭스로 표현하면 다음과 같다.
$$ \nabla \times A = \frac{1}{fgh}\begin{bmatrix}f\boldsymbol{\hat{u}} & g\boldsymbol{\hat{v}} & h\boldsymbol{\hat{w}} \\ \frac{\partial}{\partial u} & \frac{\partial}{\partial v} & \frac{\partial}{\partial w} \\ fA_u & gA_v & hA_w \end{bmatrix} $$
매트릭스 형태로 표현된 일반화된 회전공식
$$ \nabla \times A = \left( \frac{\partial A_z}{\partial y}\boldsymbol{\hat{x}} - \frac{\partial A_y}{\partial z} \right) + \left( \frac{\partial A_x}{\partial z} - \frac{\partial A_z}{\partial x} \right)\boldsymbol{\hat{y}} + \left( \frac{\partial A_y}{\partial x} - \frac{\partial A_x}{\partial y} \right)\boldsymbol{\hat{z}} $$
직교좌표계에서의 회전
$$ \nabla \times A = $$
$$ \frac{1}{r\sin{\theta}}\left[\frac{\partial}{\partial \theta}(\sin{\theta}A_{\phi}) - \frac{\partial A_{\theta}}{\partial \phi}\right]\boldsymbol{\hat{r}} $$
$$ + \frac{1}{r}\left[\frac{1}{\sin{\theta}}\frac{\partial A_{r}}{\partial \phi} - \frac{\partial }{\partial r}(rA_{\phi})\right]\boldsymbol{\hat{\theta}} $$
$$ + \frac{1}{r}\left[\frac{\partial}{\partial r}(rA_{\theta}) - \frac{\partial A_r}{\partial \phi}\right]\boldsymbol{\hat{\phi}} $$
구면좌표계에서의 회전
$$ \nabla \times A = $$
$$ \left(\frac{1}{s}\frac{\partial A_z}{\partial \phi} - \frac{\partial A_{\phi}}{\partial z}\right)\boldsymbol{\hat{s}} $$
$$ + \left(\frac{\partial A_s}{\partial z} - \frac{\partial A_{z}}{\partial s}\right)\boldsymbol{\hat{\phi}} $$
$$ + \frac{1}{s}\left[\frac{\partial }{\partial s}(sA_{\phi}) - \frac{\partial A_{s}}{\partial \phi}\right]\boldsymbol{\hat{z}} $$
원통좌표계에서의 회전
라플라시안
라플라시안은 경도의 발산이므로 계산을 해보면 다음과 같이 얻어진다.
$$ \nabla ^2 t = \frac{1}{fgh}\left[\frac{\partial}{\partial u}(\frac{gh}{f}\frac{\partial t}{\partial u}) + \frac{\partial}{\partial v}(\frac{fh}{g}\frac{\partial t}{\partial v}) + \frac{\partial}{\partial w}(\frac{fg}{h}\frac{\partial t}{\partial w})\right] $$
일반화된 라플라시안 공식
$$ \nabla ^2 t = \frac{\partial ^2 t}{\partial x^2} + \frac{\partial ^2 t}{\partial y^2} + \frac{\partial ^2 t}{\partial z^2} $$
직교좌표계에서의 라플라시안
$$ \nabla ^2 t = \frac{1}{r^2\sin{\theta}}\frac{\partial}{\partial r}(r^2\sin{\theta}\frac{\partial t}{\partial r}) + \frac{1}{r^2\sin{\theta}}\frac{\partial}{\partial \theta}(\sin{\theta}\frac{\partial t}{\partial \theta}) + \frac{1}{r^2\sin{\theta}}\frac{\partial}{\partial \phi}(\frac{1}{\sin{\theta}}\frac{\partial t}{\partial \phi}) $$
$$ = \frac{1}{r^2}\frac{\partial}{\partial r}(r^2\frac{\partial t}{\partial r}) + \frac{1}{r^2\sin{\theta}}\frac{\partial}{\partial \theta}(\sin{\theta}\frac{\partial t}{\partial \theta}) + \frac{1}{r^2\sin^2{\theta}}\frac{\partial ^2 t}{\partial \phi ^2} $$
구면좌표계에서의 라플라시안
$$ \nabla ^2 t = \frac{1}{s}\frac{\partial ^2 t}{\partial x^2} + \frac{1}{s}\frac{\partial ^2 t}{\partial y^2} + \frac{1}{s}\frac{\partial ^2 t}{\partial z^2} $$
원통좌표계에서의 라플라시안