정자계
작성일 : 2024년 04월 04일 (Thursday)
Table of contents
정자계란 자기장이 일정한 형태를 말한다.
자기력 (로렌츠 힘)
자기장 내에서 움직이는 전하 입자에 작용하는 힘을 말한다. 공식은 다음과 같다.
$$ F = Q \left[ \boldsymbol{E} + (v \times \boldsymbol{B}) \right] $$
자기력 공식. 전기장의 영향도 고려한 식이다.
자기력에 의한 일
전하에 있어서 자기력에 의한 일은 항상 0이다. 왜냐하면, 일은 $W = \boldsymbol{\widehat{F}}\cdot \boldsymbol{\widehat{l}}$로 정의가 되는데, $\boldsymbol{\widehat{l}} = \boldsymbol{\widehat{v}}dt$인데 외적은 항상 원래의 벡터와 직각이기 때문이다. 직각인 두 벡터의 내적은 0이다. 정리하면 다음과 같다.
$$ dW = \boldsymbol{\widehat{F}}\cdot \boldsymbol{\widehat{l}} = Q(v \times B) \cdot{v}dt = 0 $$
자기력에 의한 일은 0
자기력에 의한 일이 0이라는 것은 자기력은 이동하는 방향을 조금만 바꿀 뿐 이동속도를 높여주거나 줄일 수 없다는 것이다.
비오 사바르 (BIOT-SAVART LAW) 법칙
비오 사바르는 전류가 생성하는 자기장이 전류에 수직이고, 그 크기는 전선으로부터의 거리의 제곱에 반비례한다는 것이다. 자기장을 구하는 공식으로 사용된다.
정전계에서의 전기장, 전속밀도는 정자계에서 자기장, 자속밀도와 같다.
자기장의 단위는 테슬라(T)로 $1T = 1N / (A \cdot m)$이다.
$$ H = \frac{\mu _0}{4 \pi} \int \frac{I \times \boldsymbol{\widehat{\xi}}}{\xi ^2}dl^{'} = \frac{\mu _0}{4 \pi} I \int \frac{d\boldsymbol{l}^{'} \times \boldsymbol{\widehat{\xi}}}{\xi ^2} $$
자기장 공식
암페어의 법칙
자기장의 회전량은 투자율과 전기밀도의 곱이다. 이를 표현하면 다음과도 같다.
$$ \nabla \times B = \mu J $$
$$ \int (\nabla \times B) \cdot da = \oint B \cdot dl = \mu \int J \cdot da $$
$$ \oint B \cdot dl = \mu I $$
암페어의 법칙
자속밀도 B와 자기장 H
자기장 H가 가해졌을 때, 얼마나 많은 자하가 자기 분극되었는지 자속밀도를 통해 알 수 있다. 자화된 자화에 의한 자기력선이 만들어지는 데, 이 자기력선의 합을 자속이라고 하고 자속밀도란 단위부피 당 자속을 말한다. 물질마다 자화율은 다르다.
$$ \overrightarrow{H} \equiv \frac{B}{\mu _0} - M = \frac{B}{\mu _0} - \chi _m H $$
$$ H + \chi _m H = \frac{B}{\mu _0} $$
$$ B = \mu _0H + \mu _0\chi _m H = \mu _0(1 + \chi _m)H = \mu _0 \mu _r H = \mu H $$
자속밀도 식
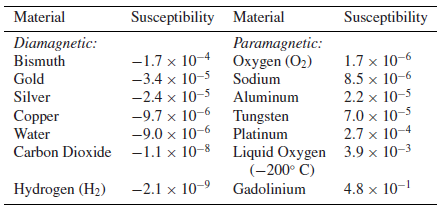
\(\chi _m\) 는 자화율이고, 자기 분극의 정도를 나타낸다.
다음은 다양한 물질 별 자화율을 나타낸다.