RLC 회로
작성일 : 2023년 01월 07일 (Saturday)
Table of contents
RLC는 수동소자이기 때문에 RLC만으로 이루어진 회로는 아무런 작동을 하지 못한다. 이번 포스트에서는 입력신호에 대해 RLC 회로의 응답을 설명한다.
임피던스(온저항 혹은 교류저항)
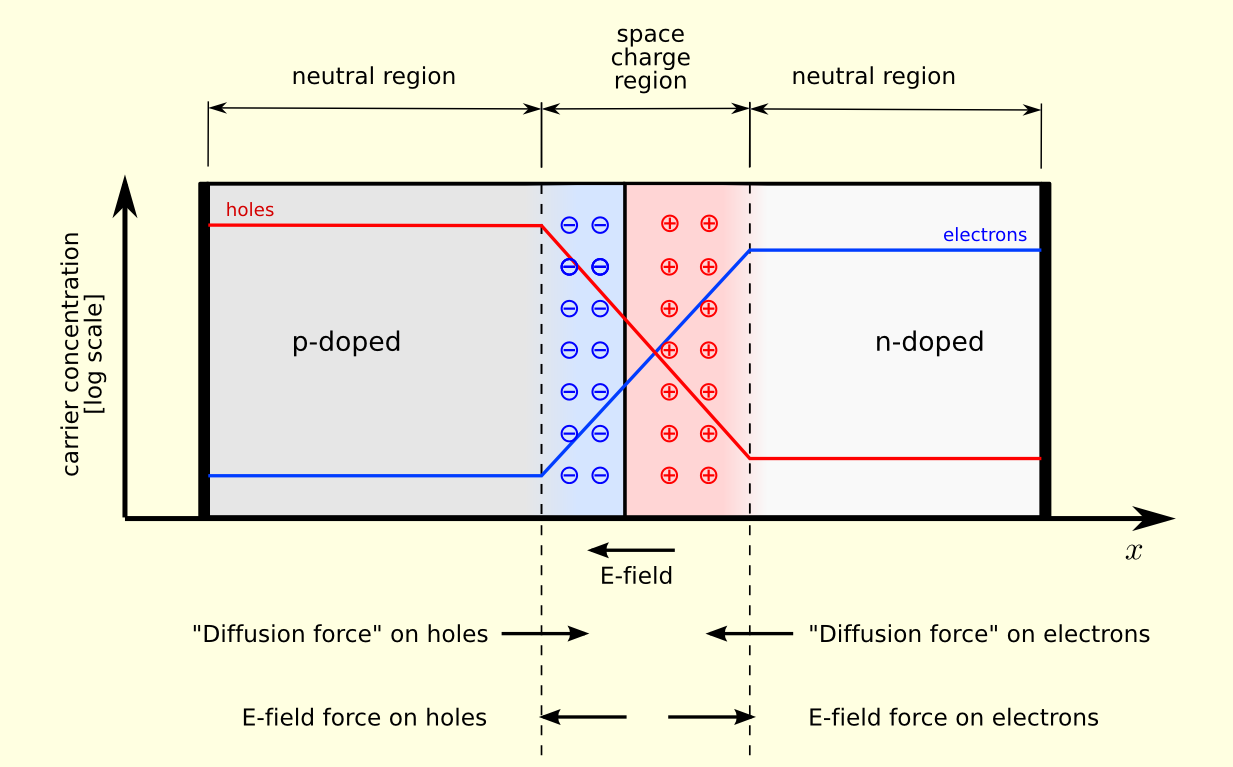
리액턴스란 말 그대로 반응이라는 뜻이다. 순수 저항은 저항만으로 이루어져있고, 커패시터와 인덕터는 각각 용량성 리액턴스 $1 \over wC$, 인덕터는 유도성 리액턴스 wL 을 가진다. 여기서 w는 각속도로 2πf 를 의미한다. 리액턴스는 주파수에 비례하는 값으로 고주파일 수록 유도성 리액턴스의 영향은 커지고 용량성 리액턴스의 영향은 작아진다. 정리하면, 고주파인 경우 유도성 리액턴스는 ∞ 로 보이고 저주파인 경우 유도성 리액턴스가 ∞ 로 보이게 된다. 임피던스란 저항과 리액턴스 성분을 모두 더한 교류저항값을 의미한다.
RC 회로 (커패시터 충방전)
커패시터의 충방전 메커니즘을 이해해보자.
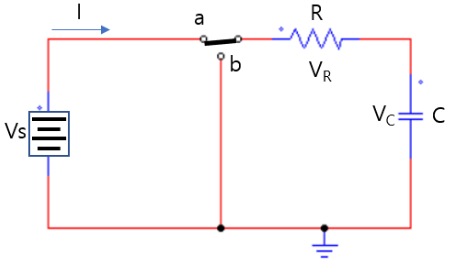
커패시터는 유전체 내의 내부 유전체가 분극되어 충전되고, 외부 전원이 제거되면 분극된 쌍극자가 다시 원래의 형태로 돌아가려고 한다. 이 때문에, 충전 방향과 방전 방향이 서로 반대이다. 아래 그림을 참조하면 충전중과 방전중 전자의 흐름이 반대임을 알 수 있다. 전류의 방향은 전자의 이동방향의 반대이다.
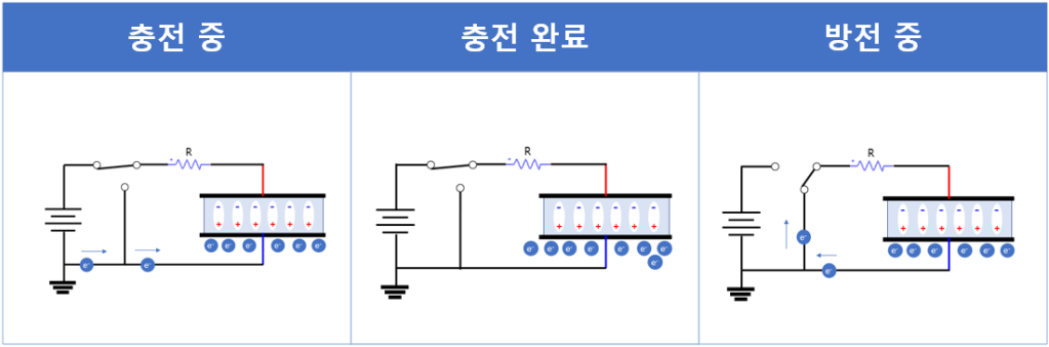
RC회로는 통상 5τ 충전하면 커패시터가 완전 충전(분극 포화 상태)된다고 생각하면 되고, 5τ 방전하면 커패시터가 거의 완전 방전된다고 생각하면 된다. (τ = RC, 단위 초) 완충시 전류는 더 이상 흐르지 않지만, 전압은 일정하게 유지된다.
충방전 식
| 상태 | 식 |
|---|---|
| 충전 (t < 0) | $V_{O}$ |
| 충전 (t ≥ 0) | $V_{S} + (V_{O} - V_{S})e^{-t/\tau}$ |
| 방전 | $v(t) = V_{O}e^{-t/RC}$ |
RL 회로 (인덕터 충방전)
인덕터의 충전을 생각해보자. 인덕터는 전류의 변화를 제어할 때 사용한다. 인덕터 역시 5τ 충전하면 커패시터가 완전 충전(자기 포화 상태), 5τ 방전하면 완전 방전 상태가 된다. 렌츠의 법칙에 의해서 유도 전류는 자기 선속의 변화를 방해하는 방향으로 충전되므로 전원의 반대 방향으로 유도전류가 형성되며 자기포화가 되면 유도 전류가 0이 된다.
충방전 식
| 상태 | 식 |
|---|---|
| 충전 (t < 0) | $I_{O}$ |
| 충전 (t ≥ 0) | $I_{S} + (I_{O} - I_{S})e^{-t/\tau}$ |
| 방전 | $i(t) = I_{O}e^{-t/RC}$ |
RLC 회로 (RLC) - 병렬회로
커패시터는 유전체에 전압이 걸려서 분극이 포화될 때까지 충전을 계속한다. 커패시터가 완전히 충전되면 유전체 내부 전기장은 일정하게 유지되고, 더 이상 전류는 흐르지 않는다. 인덕터는 전류가 흘르면 자기 포화현상이 일어날 때까지 충전된다. 자기 포화현상이 일어나면 인덕터 내부에는 자속의 변화가 없으므로 인덕터는 순수 도선처럼 동작하며 인덕터 양단의 전압이 0V가 된다. 하지만, 커패시터나 인덕터 어느 쪽에서라도 전속이나 자속이 누설되면 이 평형상태가 깨져서 전압과 전류가 진동하게 된다.
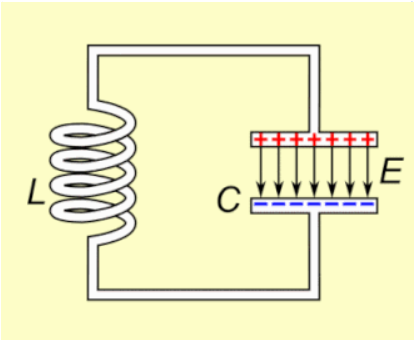
아래와 같은 RLC 병렬회로를 고려해보자.
위와 같은 LC 회로를 구성할 때, 주의할 점은 공명(또는 공진 또는 Resonance) 현상이다. 용량성 리액턴스는 1/wC로 표현되고, 유도성 리액턴스는 wL로 표현된다. 여기서 주의할 점은 용량성 리액턴스는 주파수 반비례이고, 유도성 리액턴스는 주파수 비례라는 것과, 임피던스 계산시 용량성 리액턴스는 유도성 리액턴스를 상쇄시키는 방향이라는 것이다. 따라서, 특정 주파수에서는 주파수가 0이 될 수 있다. 이 주파수가 바로 공진주파수이다.
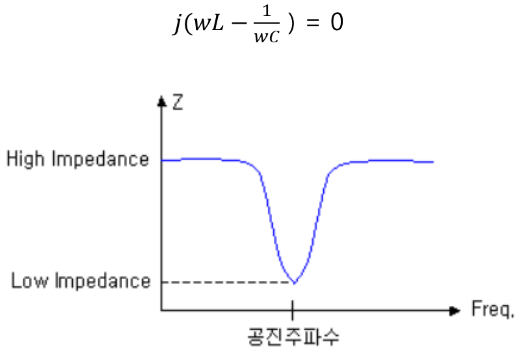
공진주파수에서는 낮은 임피던스를 갖기 때문에 순간적으로 전류의 진폭이 증가한다.
LC 회로 (RLC) - 직렬회로
직렬회로는 공진주파수에서 오히려 임피던스가 무한대로 발산한다는 점이 다르다. 공진주파수에서는 개방회로로 동작한다.
