전달함수와 상태공간
작성일 : 2025년 05월 26일 (Monday)
전달함수
시스템이라는 개념은 이전글에서 알게되었을 것이고, 그러면 시스템을 수학적으로 표현하는 방법은 무엇일까? 전달함수를 사용하면 시스템을 수학적으로 표현할 수 있다. 전달함수는 말 그대로 특정 입력이 들어왔을 때 시스템의 출력은 어떻게 되는지를 표현한 함수이다. 전달함수는 s-평면 상에 표현한다는 부분 말고 우리가 흔히 사용하던 y=f(x), x=f(t) 등과 다를게 없다.
s-평면
s-평면은 무엇일까? “s”는 라플라스 변환에서 사용하는 “s”, 그 “s”가 맞다. 우리는 시간축으로 표현하기 어려운 것들을 주파수로 변환해서 분석하기 위해서 라플라스 변환, 푸리에 변환 (라플라스 변환의 가장 간단한 버전 σ = 0) 을 사용했었다. 주파수 응답(사인파 인가시의 응답)을 보는 이유는 시계열 데이터로 보았을 때는 규칙은 보이지만 식으로 표현하기 어려웠던 부분들을 주파수 응답으로는 간단하게 표현이 가능하기 때문이다. 즉, 이러한 이점을 이용하기 위해서 우리는 전달함수를 s-평면 상에 그려보는 것이다.
입력 X(s)에 대해 출력이 Y(s)로 나타나고 그 때의 전달함수가 G(s)인 LTI 시스템을 고려해보자. 그러면 관계식은, Y(s) = G(s)X(s)로 나타낼 수 있다. 라플라스 변환식에서의 곱셈은 역변환에서는 컨벌루션이므로 시간 t로 다시 역변환하게 되면 다음과 같이 표현된다.
$$ Y(s) = G(s)X(s) $$
$$ y(t) = \int_{0}^{t} x(\tau) g(t - \tau)d\tau $$
라플라스 역변환
컨볼루션은 다음과 같이 LTI 시스템에 대해서 모든 입력을 전달함수와 곱해서 누적한 적분을 말한다. 특정 시점에서 출력이 얼마인지 계산하려면 라플라스 변환을 통해 간단하게 변환한 방정식을 풀어서 G(s)를 s에 대해 표현하고 역변환을 통해 g(t)를 구하면 된다.
상태공간 (State Space)
특정 시스템이 구분지을 수 있는 특정한 상태가 되도록 하는 변수들의 최소한의 조합을 상태변수(State Variables)라고 한다. 즉, 어떤 시스템이 n개의 변수로 모든 상태를 표현할 수 있다면 그 n개의 변수는 모두 상태변수가 된다. 이러한 상태변수를 벡터로 표현한 것이 상태 벡터(State Vector)이다. 상태벡터를 통해 입력이 들어왔을 때의 출력을 알 수 있다. 이 상태벡터를 축으로 하여 생성된 Span이 상태공간(State Space)이 된다. 상태는 상태공간의 한 점으로 표현된다.
상태변수와, 상태공간을 더 잘 이해하기 위해서 스팬(Span)에 대해서 되짚어볼 필요가 있다. 스팬은 아래 그림처럼 벡터에 스칼라를 곱해서 만들 수 있는 영역을 말한다. 상태공간 방정식에서 특정 상태는 공간상의 한점이라고 했는데, 선형독립인 벡터들로 스팬을 만들면 더 높은 차원의 공간으로 확장되기 때문에 특정 위치를 찾는게 더욱 복잡해지는 것이다. 다른 말로는 미지수가 1개인 방정식을 풀면 됐는데, 선형독립인 상태변수가 늘어날 때마다 미지수가 하나씩 더 늘어나서 연립방정식의 해를 구해야하게 되는 것이다. 안타깝게도 우리가 다루는 상태공간 방정식의 상태변수는 모두 선형독립인 벡터들의 조합이어서 더 이상 간단하게 줄이는 것이 불가능하다. 즉, 변수가 늘어날수록 기하급수적으로 답을 찾는게 어려워지므로 문제를 풀 때 불필요한 변수는 과감하게 버리는게 좋은 선택지일 수 있다.
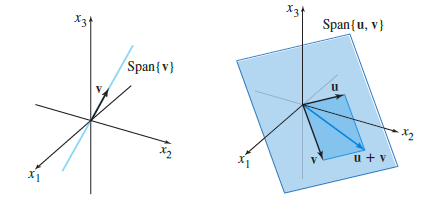

상태공간 방정식
이러한 상태공간을 고려한 방정식이 아래의 상태공간 방정식이다.
$$ \dot{x}(t) = \mathsf{A}x(t) + \mathsf{B}u(t) \tag{1} $$
$$ y(t) = \mathsf{C}x(t) + \mathsf{D}u(t) \tag{2} $$
상태공간 방정식 (1)과 출력식 (2)
x(t)는 상태변수이고 나타내고, $\dot{x}(t)$ 는 상태변수가 변화하는 정도를 나타낸다. $\mathsf{A}$는 현재 상태가 다음 상태 변화에 영향을 미치는 정도를 나타내고, $\mathsf{B}$는 현재 입력이 다음 상태 변화에 영향을 미치는 정도를 나타내고, $\mathsf{C}$는 현재 상태가 출력에 어떻게 영향을 미치는지 나타내고, $\mathsf{D}$는 현재 입력이 시스템을 거치지 않고 직접 출력에 어떻게 영향을 미치는지를 나타낸다. 일반적으로 제어가능한 형태의 상태공간방정식의 D의 값은 모두 0이다. (피드포워드가 없는 경우 0) 상태공간을 사용하는 이유는 다중입력, 다중출력에 대해서 값을 계산하기 용이하기 때문에 그렇다.
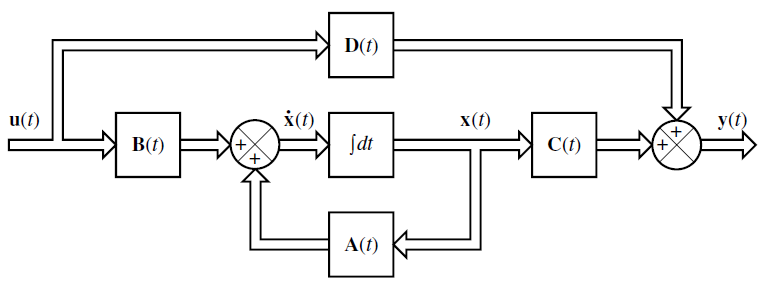

예시
탄성 계수 k를 갖는 용수철에 매달린 질량 m 물질이 감쇠계수 b를 갖는 서스펜션에 연결된 아래의 경우를 생각해보자.
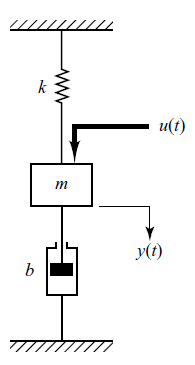

위 식은 입력 u (아래로 누르는 힘)이 있을 때, 변위 y는 얼마나 될지를 구해보자.
$$ m\ddot{y} + b\dot{y} + ky = u $$
관계식
용수철에 의한 힘은 -k × 변위 이고, 서스펜션(댐퍼)에 의한 감쇠력은 -b × 속도를 말한다. 물체에 가해진 힘은 m * a (이번의 경우 g)이다. 이를 상태공간 방정식을 이용해 나타내보자.
속도 $\dot{y}$, 변위 $y$는 $x_{2}$, $x_{1}$ 으로 나타낼 수 있고, 가속도 $\ddot{y}$, 속도 $\dot{y}$는 각각 상태변수의 미분식을 활용해서 \(\dot{x}_{2}\), \(\dot{x}_{1}\) 로 나타낼 수 있다. 그렇게 되면 위 식은 다음과 같이 정리된다.
$$ \dot{x}_{1} = x_{2} \tag{1} $$
$$ \dot{x}_{2} = -\frac{k}{m}x_{1} - \frac{b}{m}x_{2} + \frac{1}{m}u \tag{2} $$
$$ y = x_{1} \tag{3} $$
상태공간 방정식 (1, 2)과 출력식 (3)
이를 행렬 방정식 형태의 상태공간 방정식으로 표현하면 다음과 같이 정리된다.
$$ \begin{bmatrix} \dot{x}_{1} \\ \dot{x}_{2} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{b}{m} \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{m} \end{bmatrix} u $$
행렬 방정식 형태의 상태공간 방정식
$$ y = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix} $$
행렬 방정식 형태의 출력 방정식
$$ \mathsf{A} = \begin{bmatrix} 0 & 1 \\ -\frac{k}{m} & -\frac{b}{m} \end{bmatrix} $$
$$ \mathsf{B} = \begin{bmatrix} 0 \\ \frac{1}{m} \end{bmatrix} $$
$$ \mathsf{C} = \begin{bmatrix} 1 & 0 \end{bmatrix} $$
$$ \mathsf{D} = 0 $$
정리


