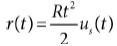기호 및 원형 함수
작성일 : 2023년 01월 23일 (Monday)
공대수학에서 사용하는 기호들에 대한 정리이다. 빠져있는 부분들이 있으면 조금씩 더 추가해 나갈 예정이다.
뻔한 기호들은 제외하였다.
기호
| 기호 | Latex | 이름 | 의미 | 예시 | 읽는법 |
|---|---|---|---|---|---|
| $\in $ | \in | Belong to/is an element of | 속함 | - | - |
| $\forall$ | \forall | for all | 모든 | - | - |
| $\Leftrightarrow$ | \Leftrightarrow | equivalent | 동등 | - | - |
| $\exists$ | \exists | there exists | 존재 | - | - |
| $\because$ | \because | because | 왜냐하면 | - | - |
| $\therefore$ | \therefore | therefore | 그러므로 | - | - |
| s.t | - | such that | ~를 만족하도록 하는 | - | - |
| $L^{1}$ | - | Lebesgue Space 1 | 르베그 공간 1 : 1차 적분가능 | $L^{1}(\mathbb{R})$ | - |
| $L^{2}$ | - | Lebesgue Space 2 | 르베그 공간 2 : 2차 (제곱) 적분가능 | $L^{2}(\mathbb{R})$ | - |
| $L^{p}$ | - | Lebesgue Space p | 르베그 공간 p : p차 적분가능 | $L^{p}(\mathbb{R})$ | - |
| ${\mathbb{R}}$ | - | Real Number Space | 실수 공간 | - | ${\mathbb{R}}^2$ : r-two |
| ${\mathbb{N}}$ | - | Natural Number Space | 자연수 공간 | - | - |
| ${\mathbb{Z}}$ | - | Integers Space | 정수 공간 | - | - |
| ${\mathbb{Z}}_p$ | - | p-adic Interges Space | p-adic 정수 공간 | - | - |
| ${\mathbb{Q}}$ | - | Rational Number Space | 유리수 공간 | - | - |
| ${\mathbb{Q}}_p$ | - | p-adic Rational Number Space | p-adic 유리수 공간 | - | - |
| ${\mathbb{C}}$ | - | Complex Number Space | 복소수 공간 | - | - |
함수
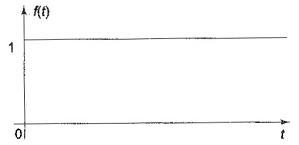
단위계단함수 (Unit Step Function) u(t)
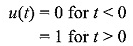
(좌클릭 : 확대 / 우클릭 : 축소)
× 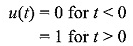
(좌클릭 : 확대 / 우클릭 : 축소)
× 
단위경사함수 (Unit Ramp Function) r(t)
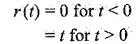
(좌클릭 : 확대 / 우클릭 : 축소)
× 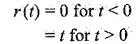
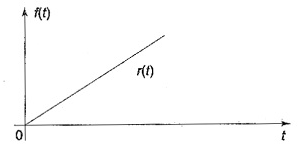
(좌클릭 : 확대 / 우클릭 : 축소)
× 
단위충격함수 (Unit Impulse Funciton) $\delta$(t)
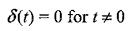
(좌클릭 : 확대 / 우클릭 : 축소)
× 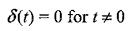
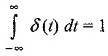
(좌클릭 : 확대 / 우클릭 : 축소)
× 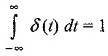

(좌클릭 : 확대 / 우클릭 : 축소)
× 
쌍곡선함수 (Parabolic Function)
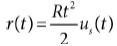
(좌클릭 : 확대 / 우클릭 : 축소)
×