인덕터 원리/구조
작성일 : 2023년 06월 18일 (Sunday)
Table of contents
인덕터는 고주파를 억제하는 성분을 가진다. 그리고 유도성 리액턴스를 가지기 때문에 전류의 위상이 전압의 위상보다 90도 뒤진다는 특성을 가지고 있기도 하다.
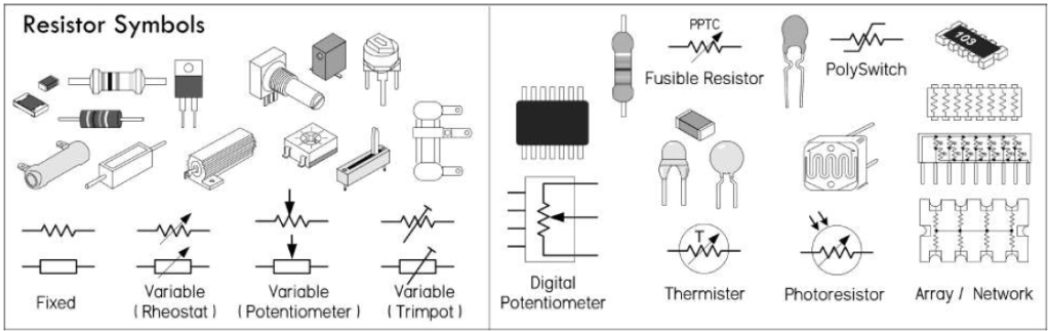
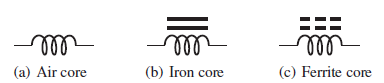
인덕터는 회로기호로는 아래와 같이 표현한다. 인덕터 내부 코어에 따라 다르게 표시하기도 한다.

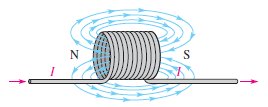
인덕터는 전류가 흐르면 자기장이 발생하게 되는데 이 자기장은 오른 나사 법칙에 따라 자기장의 방향이 결정된다.

인덕턴스
인덕턴스가 높을 수록 전류가 변화할 때 인덕터 양단에 걸리는 전압의 크기가 증가한다. 인덕턴스의 단위는 헨리 H (Henry)이다. 1헨리는 1A의 전류가 도선에 흘렀을 때 생성되는 자속의 크기를 의미한다.
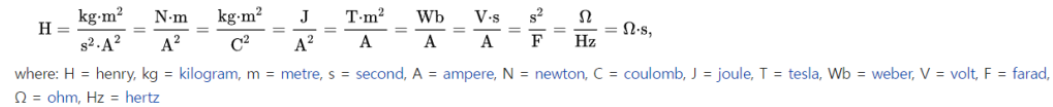
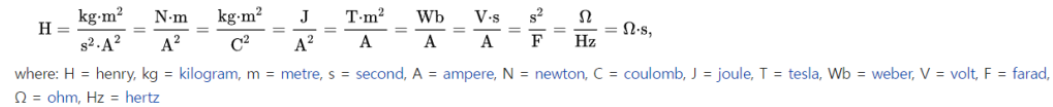
인덕턴스, 전류, 코일 턴수, 자속은 $LI = N\phi = \Phi$의 관계를 갖는다.
자속 : 특정 평면을 통과하는 자기력선을 모두 더한 값
인덕터 구조 별 인덕턴스 공식
기자력(m.m.f)과 자기저항, 자속에 대한 식을 참고하면 인덕턴스에 새로운 공식을 유도할 수 있다. 자세한 내용은 이전에 포스팅한 전기기기 기초을 참고하면 될 것 같다. 그 식을 가져오면, 아래 (1), (2), (3)와 같다. (3)식은 (1)식에 (2)식을 대입하고 정리한 것이다.
$$ \phi = \frac{m.m.f}{\mathfrak{R}} = \frac{NI}{\mathfrak{R}} \tag{1} $$
$$ R = \frac{l}{\mu S} \tag{2} $$
$$ \phi = \frac{\mu SNI}{l} \tag{3} $$
두 식을 이용하여 $LI = N\phi$를 잘 변형하면 인덕턴스를 길이, 면적, 턴수에 대해서 표현할 수 있다. (4)식에 (1)식을 대입하여 정리하면 (5)식이 얻이진다. 그리고 최종적으로 (5)식에 (2)식을 적용하면 최종적인 형태인 (6)식이 얻어진다.
$$ L = \frac{N\phi}{I} \tag{4} $$
$$ L = \frac{N^{2}}{R} \tag{5} $$
$$ L = \frac{\mu SN^{2}}{l} \tag{6} $$
(6)식을 이용하면 인덕터의 길이, 단면적, 턴수에 따른 인덕턴스를 계산할 수 있게된다.
상호 인덕턴스 M : 변압기의 원리
상호 인덕턴스란 두 인접한 인덕터가 있다고 가정했을 때, 하나의 인덕터에 전류가 흘러 발생한 자속에 의해 다른 인덕터에도 자속이 유도되는 정도를 의미한다. 지금까지는 인덕터 자기자신의 자기 인덕턴스만을 고려했지만, 사실 인덕터는 외부의 자기장을 받아들여서 전기를 만들어내기도 하기 때문에 인덕터 여러개가 가까이 붙어있으면 다른 인덕터에서 생성시킨 자기장을 다른 인덕터에서 가져다 쓸 수도 있다. 변압기, 릴레이 등 여러가지 소자에서 이 상호 인덕턴스의 원리를 이용하고 있다고 보면 된다.
이 상호 인덕턴스는 $M = \sqrt{L_{1}L_{2}}$로 표현되는데, 실제로는 코어를 자화시키는데도 전류가 소모되고 와전류 등으로 인한 철손도 고려해야 하기 때문에 실제로는 1보다 작은 결합계수를 곱한 형태인 $M = k\sqrt{L_{1}L_{2}}$와 같이 사용한다.
인덕터 1, 인덕터 2가 있고 각각의 인덕턴스가 $L_1$, $L_2$ 이고 상호인덕턴스가 $M$이라고 할 때, 상호인덕턴스를 고려한 인덕턴스 2의 전압은 $V_2 = L_2\frac{di_2}{dt} + M\frac{di_1}{dt}$가 된다.
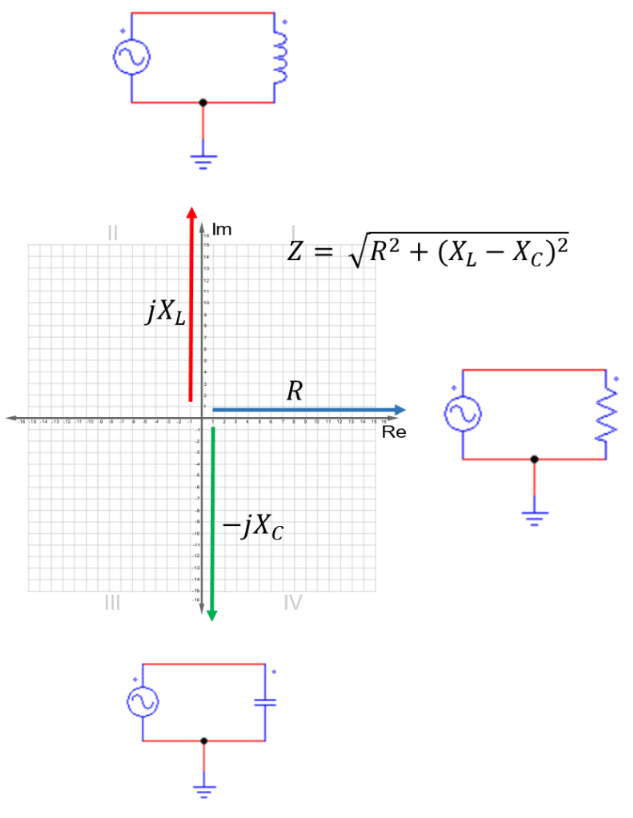
인덕터에 의한 위상 변화
인덕터는 유도성 리액턴스를 가진다. 전압에 의해서 인덕터 주변에 자속이 생성되고, 자기포화 상태가 되면 그 값을 유지한다. 이전에 RLC 를 페이저로 표현했을 때 유도성 리액턴스는 +90도의 위상을 가진다고 했는데, $\frac{V}{I} = Z$ 이므로 전압이 전류 대비 +90도의 위상을 가진다는 것을 의미하고, 다른 말로 전압이 전류보다 90도 앞선다는 것을 뜻한다.

인덕턴스의 합성 (병렬과 직렬)
상호 인덕턴스의 합성은 저항과 동일하다. 직렬연결은 더하고, 병렬연결은 역수를 취한 것의 합을 다시 역수를 취한다.
상호 인덕턴스를 고려하면, 하나의 코어에 두개의 코일을 감는 경우, 코일의 감는 방향, 접속점에 따라서 같은양의 코일, 같은 턴수를 적용해도 상호 인덕턴스에 의해서 총 인덕턴스가 달라질 수도 있다는 것을 알 수 있다. 코일을 계속해서 같은 방향으로 감는 것을 가동 결합, 반대로 감는 것을 차동결합이라고 한다. 인덕터 2개를 결합한다고 가정했을 때, 인덕터 1의 인덕턴스를 $L_1$, 인덕터 2의 인덕턴스를 $L_2$, 상호 인덕턴스를 M이라고 하면 다음과 같다. 각각의 인덕턴스 합성 공식에 대한 증명도 첨부한다.
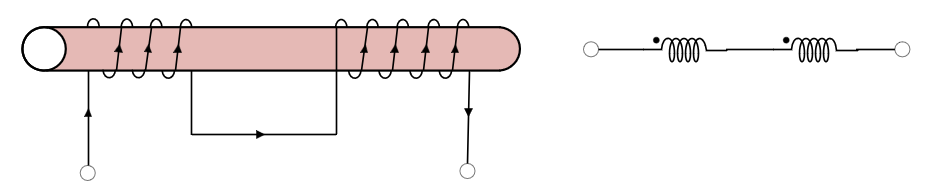

직렬 가동결합시 인덕턴스 : $L = L_1 + L_2 + 2M$
$$ v_1 = L_1\frac{di_1}{dt} + M\frac{di_2}{dt} $$
$$ v_2 = L_2\frac{di_2}{dt} + M\frac{di_1}{dt} $$
$$ v = v_1 + v_2 \tag{1} $$
$$ v = L_1\frac{di_1}{dt} + M\frac{di_2}{dt} + L_2\frac{di_2}{dt} + M\frac{di_1}{dt} \tag{2} $$
$$ v = (L_1 + L_2 + 2M)\frac{di}{dt} \tag{3} $$
직렬 가동결합 인덕턴스 합성 증명
두 인덕터에 의해 생성된 전압을 v라고 하면, 이 v는 두 인덕터의 전압을 더한 전압이 된다. 근데 직렬이므로 두 인덕터에 흐르는 전류가 서로 같아서 그 전류를 i라고 하면 최종적으로 (3)식이 얻어져 합성 임피던스는 $L_1 + L_2 + 2M$이 된다.
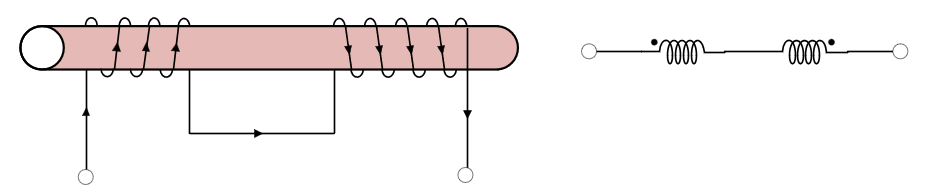

직렬 차동결합시 인덕턴스 : $L = L_1 + L_2 - 2M$
$$ v_1 = L_1\frac{di_1}{dt} - M\frac{di_2}{dt} $$
$$ v_2 = L_2\frac{di_2}{dt} - M\frac{di_1}{dt} $$
$$ v = v_1 + v_2 \tag{1} $$
$$ v = L_1\frac{di_1}{dt} - M\frac{di_2}{dt} + L_2\frac{di_2}{dt} - M\frac{di_1}{dt} \tag{2} $$
$$ v = (L_1 + L_2 - 2M)\frac{di}{dt} \tag{3} $$
직렬 차동결합 인덕턴스 합성 증명
두 인덕터에 의해 생성된 전압을 v라고 하면, 이 v는 두 인덕터의 전압을 더한 전압이 된다. 근데 직렬이므로 두 인덕터에 흐르는 전류가 서로 같아서 그 전류를 i라고 하면 최종적으로 (3)식이 얻어져 합성 임피던스는 $L_1 + L_2 - 2M$이 된다.
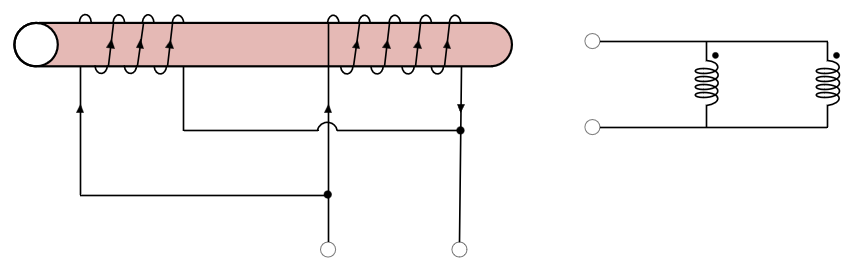

병렬 가동결합시 인덕턴스 : $L = \frac{L_1L_2 - M^2}{L_1 + L_2 - 2M}$
$$ v_1 = L_1\frac{di_1}{dt} + M\frac{di_2}{dt} \tag{1} $$
$$ v_2 = L_2\frac{di_2}{dt} + M\frac{di_1}{dt} \tag{2} $$
$$ i = i_1 + i_2 \tag{3} $$
$$ ((3) 미분) : \frac{di}{dt} = \frac{di_1}{dt} + \frac{di_2}{dt} \tag{4} $$
$$ v = v_1 = v_2 \tag{5} $$
$$ ((1) \times L_2) : L_2v = L_1L_2\frac{di_1}{dt} + L_2M\frac{di_2}{dt} \tag{6} $$
$$ ((2) \times M) : Mv= ML_2\frac{di_2}{dt} + M^2\frac{di_1}{dt} \tag{7} $$
$$ ((6) - (7)) : (L2 - M)v = L_1L_2\frac{di_1}{dt} - M^2\frac{di_1}{dt} $$
$$ \frac{di_1}{dt} = \frac{L_2 - M}{L_1L_2 - M^2}v \tag{8} $$
$$ \frac{di_2}{dt} = \frac{L_1 - M}{L_1L_2 - M^2}v \tag{9} $$
$$ ((4) \leftarrow (8), (9)) : \frac{di}{dt} = \frac{L_1 + L_2 - 2M}{L_1L_2 - M^2}v $$
$$ v = L\frac{di}{dt} $$
$$ \therefore L = \frac{L_1L_2 - M^2}{L_1 + L_2 - 2M} $$
병렬 가동결합 인덕턴스 합성 증명
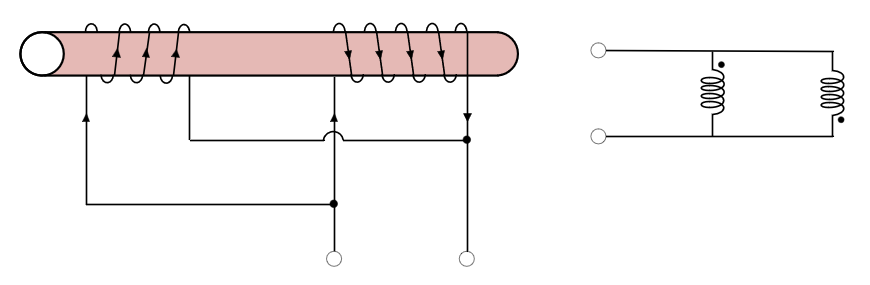

병렬 차동결합시 인덕턴스 : $L = \frac{L_1L_2 - M^2}{L_1 + L_2 + 2M}$
$$ v_1 = L_1\frac{di_1}{dt} - M\frac{di_2}{dt} \tag{1} $$
$$ v_2 = L_2\frac{di_2}{dt} - M\frac{di_1}{dt} \tag{2} $$
$$ i = i_1 + i_2 \tag{3} $$
$$ ((3) 미분) : \frac{di}{dt} = \frac{di_1}{dt} + \frac{di_2}{dt} \tag{4} $$
$$ v = v_1 = v_2 \tag{5} $$
$$ ((1) \times L_2) : L_2v = L_1L_2\frac{di_1}{dt} - L_2M\frac{di_2}{dt} \tag{6} $$
$$ ((2) \times M) : Mv= ML_2\frac{di_2}{dt} - M^2\frac{di_1}{dt} \tag{7} $$
$$ ((6) + (7)) : (L2 + M)v = L_1L_2\frac{di_1}{dt} - M^2\frac{di_1}{dt} $$
$$ \frac{di_1}{dt} = \frac{L_2 + M}{L_1L_2 - M^2}v \tag{8} $$
$$ \frac{di_2}{dt} = \frac{L_1 + M}{L_1L_2 - M^2}v \tag{9} $$
$$ ((4) \leftarrow (8), (9)) : \frac{di}{dt} = \frac{L_1 + L_2 + 2M}{L_1L_2 - M^2}v $$
$$ v = L\frac{di}{dt} $$
$$ \therefore L = \frac{L_1L_2 - M^2}{L_1 + L_2 + 2M} $$
병렬 차동결합 인덕턴스 합성 증명
상호 인덕턴스를 고려하게 되면 식이 복잡해질 수 있으므로 무시할 수 있는 정도의 양이면 무시하는게 속 편하다.
자화와 투자율
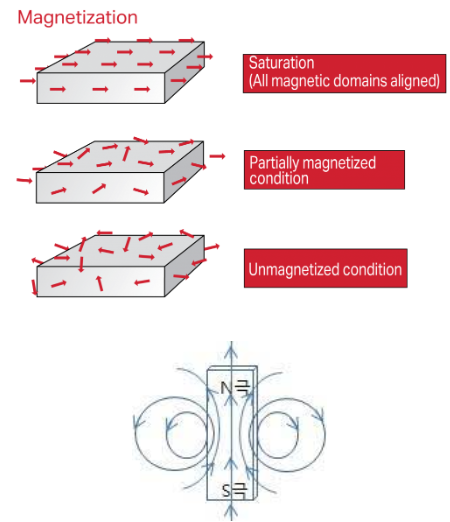
자계에서도 분극과 비슷한 개념이 존재한다. 바로 자화인데, 아래와 같이 자기쌍극자가 자기장의 방향에 따라 자기 쌍극자가 배열되는 현상을 말한다. 매질에서 이 자화가 일어나는 정도를 자화율이라고 하고, 그 값은 매질에 따라 다르다. 투자율은 자화율에 1을 더한 값에 자유공간에서의 투자율을 곱한 값으로 매질에 자기장이 가해졌을 때, 얼마만큼의 자속이 생성되는 지를 의미하는 값이다.
$$ 1 + {\chi}_{m} = {\mu}_{r} = \frac{\mu}{\mu _{0}} $$
$$ \overrightarrow{B} = {\mu}_{0}(1 + {\chi}_{m})\overrightarrow{H} = {\mu}_{0}{\mu}_{r}\overrightarrow{H} = \mu \overrightarrow{H} $$
B는 자속밀도, H는 자기장을 의미한다.
자화율, 상대투자율은 단위가 없는 상수.
투자율 단위 H/m, 자속밀도 단위 T = Wb/m2, 자기장 단위 A/m

오른나사의 법칙
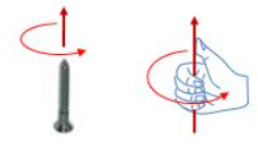

전류가 자계를 발생시키는 관계를 오른나사에 비유한 법칙. 코일에 흐르는 전류의 방향으로 도선 코일 중심의 자속의 방향을 알 수 있다. 이해가 안된다면 위의 전류에 따른 자기력선의 방향 그림도 함께 참고해보자. 아래의 코일 간의 자기력선 상쇄 효과 그림도 참고해보면 전류에 따른 자기력선의 방향 그림은 결국 각각의 코일의 자기력선 상쇄효과를 요약해놓은 것이라고 볼 수 있다.
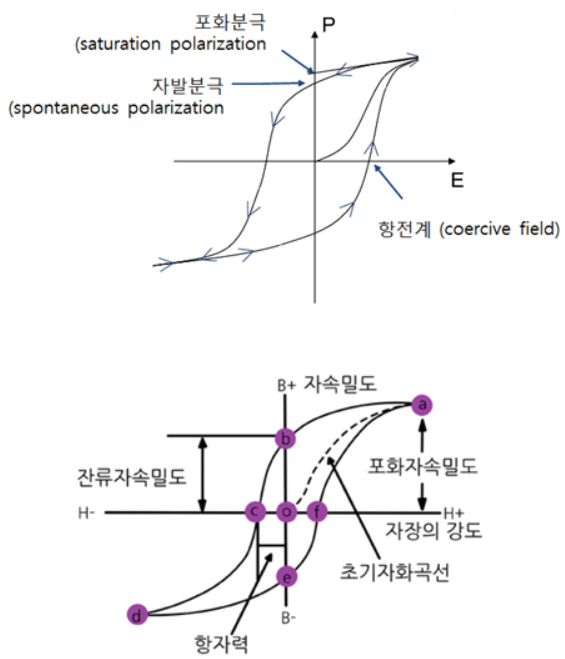
자기포화
자성체에 자기장이 가해지면 자기 분극이 일어나는데, 모든 자기 쌍극자가 분극되면 자기장이 더 강하게 가해져도 더 이상 분극이 추가로 일어나지 않는다. 이를 자기 포화라고 하는데 이렇게 되면 더 이상 자속이 증가하지 않는다. 주로 강자성체에서 발생하는 현상으로, 코어를 강자성체를 사용한 인덕터를 사용하면 전류의 크기를 키워도 코어가 이미 자기포화 상태라면 전류를 더 흘려도 자기포화에 의해서 자속이 증가하지 않는다. 자기포화는 변압기에서 공극을 사용하는 이유가 되기도 한다. 코어에 공극을 삽입하면 자기포화가 발생하지 않는다.