푸리에 시리즈 (연속시간)
작성일 : 2025년 05월 11일 (Sunday)
Table of contents
연속시간 푸리에 시리즈 (CTFS)
주기함수를 아래와 같이 삼각함수의 가중치로 분해하여 주파수 스펙트럼 상에서 신호를 분석하는 데 사용된다. 연속적인 주기함수를 이산적인 주파수의 합으로 표현하여 각 주파수에서의 위상과 크기를 확인할 수 있다는 특징이 있다. 주기적인 파형이 발생하면 그 파형의 주기 T를 측정하여, 한 주기에 대해서 CTFS를 수행하면 여러개의 삼각함수와 가중치로 분리할 수 있어서, 주파수별 위상과 크기를 확인할 수 있다. 아래서는 모두 \(\frac{2\pi}{T}\) 로 표현했는데, 더 일반적으로는 기본 각주파수 \(w_{0}\) 로 표현되니 참고하자. 이 글에서는 이해를 돕기 위해 \(\frac{2\pi}{T}\)를 사용하였다.
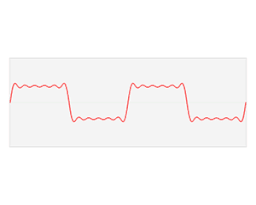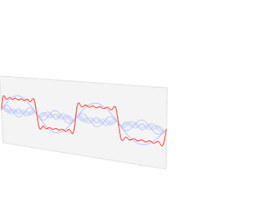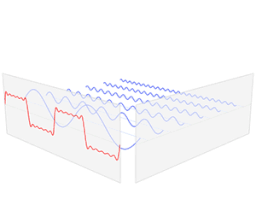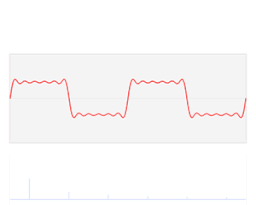



아래는 주기가 T인 함수 f(t)를 푸리에 시리즈로 표현한 것이다. 아래 (1), (2)는 복소 정현파를 오일러 공식을 이용해 각각 $\cos(\theta)$, $\sin(\theta)$에 대해 정리한 것이고, (1), (2)를 $f(t)$의 푸리에 시리즈에 대입하면 (3)식이 얻어진다.
$$ \widetilde{f}(t) \backsimeq a_0+\sum_{k=1}^\infty a_k\cos\left(\frac{2\pi k t}{T}\right)+\sum_{k=1}^{\infty} b_k \sin\left(\frac{2\pi k t}{T}\right) $$
$$ \cos(\theta) = \frac{\exp(j\theta)+\exp(-j\theta)}{2} \tag{1} $$
$$ \sin(\theta) = \frac{\exp(j\theta)-\exp(-j\theta)}{2j} \tag{2} $$
$$ \widetilde{f}(t) \backsimeq a_0+\sum_{k=1}^{\infty}\left(a_k\frac{\exp\left(j 2\pi k t/T\right)+\exp\left(-j2\pi k t/T\right)}{2}+ b_k\frac{\exp\left(j 2\pi k t/T\right)-\exp\left(-j 2\pi k t/T\right)}{2j}\right) $$
$$ =a_0+\sum_{k=1}^{\infty}\left(\frac{a_k-jb_k}{2}\exp\left(j\frac{2\pi k t}{T}\right)+\frac{a_k+jb_k}{2}\exp\left(-j\frac{2\pi kt}{T}\right)\right) $$
$$ = \sum_{k=-\infty}^{\infty}c_k\exp\left(j\frac{2\pi k t}{T}\right) \tag{3} $$
$$ c_k = \begin{cases}\frac{1}{2}(a_k-jb_k),&& k >0 \\ a_0, && k = 0\\ \frac{1}{2}(a_k+jb_k), && k < 0 \end{cases} $$
$$ c_k = \frac{1}{T}\int_{0}^{T}\widetilde{f}(t)\exp\left(-j\frac{2\pi k t}{T}\right)dt $$
Analysis Equation
$$ \widetilde{f}(t)=\sum_{k=-\infty}^{\infty}c_k\exp\left(j \frac{2\pi k t}{T}\right)=\sum_{k=-\infty}^{\infty}c_k\exp\left(j w_{0} k t\right) $$
Synthesis Equation
푸리에 시리즈에서 복소 정현파를 사용하는 이유 (페이저)
함수의 내적을 이용하면 두 함수 간의 유사성을 확인할 수 있는데, 주파수가 다른 두 복소 정현파의 내적은 항상 0(직교)이기 때문에 푸리에 시리즈에서 정현파를 기저신호로 사용한다.
$$ \lt f(t), g(t) \gt = \int_{a}^{b}f(t)g^*(t) dt= 0 $$
함수의 내적
$$ \lt \exp\left(j\frac{2\pi at}{T}\right), \exp\left(j\frac{2\pi bt}{T}\right)\gt $$
$$ =\int_{0}^{T}\exp\left(j\frac{2\pi at}{T}\right)\exp\left(-j\frac{2\pi bt}{T}\right)dt $$
$$ =\int_{0}^{T}\exp\left(j\frac{2\pi (a-b)t}{T}\right)dt = \int_{0}^{T}\exp\left(j\frac{2\pi kt}{T}\right)dt $$
$$ = \frac{T}{j2\pi k}\left|\exp\left(j\frac{2\pi k t}{T}\right)\right|_{0}^{T}=\frac{T}{j2\pi k}(\exp(j2\pi k) - \exp(0)) = \frac{T}{j2\pi k}(1-1) = 0 $$
주파수가 다른 복소 정현파의 내적
이 직교하는 $\sin$과 $\cos$ 두 정현파를 복소수에 대한 벡터로 나타냈을 때 서로 선형독립관계에 있어서 벡터공간을 만들기 때문에 푸리에 시리즈를 벡터공간에 맵핑할 수 있는데, 이 것이 바로 페이저다. 페이저를 사용하면 길이가 무한한 주기가 동일한 함수를 유한한 크기의 원에 회전시켜 감아서 표현하여 한 눈에 정리할 수 있기 때문에 복소 정현파를 사용한다. 이 내용을 이해하기 위해서는 이 글을 차분히 끝내고, 다음 글인 푸리에 변환을 참고하길 바란다.
부분 합 ($S_{N}$)
하지만, 현실적으로 끝이 없는 무한대의 삼각함수를 모두 더하는 것은 불가능하다. 따라서, 어느 정도의 오차를 감안하고 부분합으로 사용하는 것이 가장 일반적이다. 부분합은
$$ S_{N}(f) = \sum_{n=-N}^{N}{c_{n}\exp\left({\frac{2\pi njt}{N}}\right)} $$
푸리에 시리즈 부분합
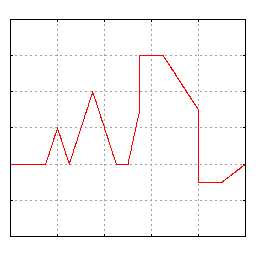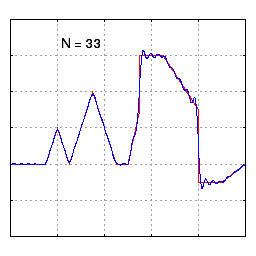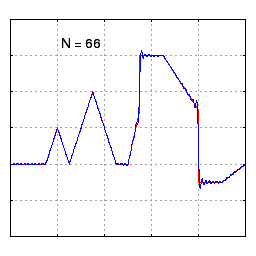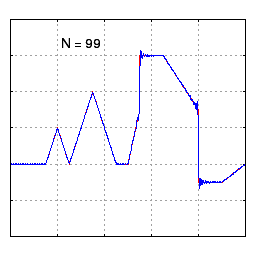

부분합의 수렴 (디리클레 (Dirichlet) 조건)
푸리에 시리즈의 부분합을 실제로 사용하려면 수렴 조건을 이해하고 있어야 한다. 여기서의 수렴은 Limit 값을 취해서 특정 값으로 수렴한다는 의미는 아니고, 부분합 $S_N$이 f(x)에 거의 근접한다는 말로 사용된다. 다른말로 이야기하면, 수렴한다는 의미는 각 주파수에서의 크기와 위상을 대략적으로 알 수 있다는 의미이다.
$$ S(x) = \lim_\limits{N \to \infty} S_N (x) \Rightarrow S_N (x) \simeq \frac{a_0}{2} + \sum_{n = 1}^{N-1}(a_n{\cos{nx}}+b_n{\sin{nx}}) $$
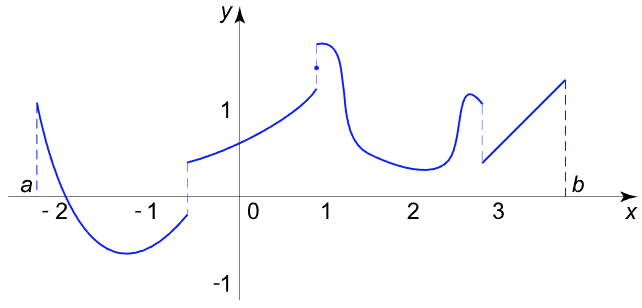
디리클레 조건을 만족하면 수렴조건을 만족한다고 할 수 있다. 디리클레 조건이란 단가함수이면서, 유한개의 불연속점을 가지고, 절대 적분가능 (유한한 에너지) 함을 말한다. 디리클레 조건을 만족하면 점별수렴은 만족한다고 볼 수 있지만 균등수렴(수렴값에 도달하는 속도가 모든 정의역에 대해 동일한 경우)은 보장하지 못하고, 디리클레 조건을 만족하지 않더라도 점별수렴할 수 있다. 디리클레 조건은 점별수렴을 위한 충분조건이지, 필요조건이 아니기 때문이다. 하지만, 일반적으로 디리클레 조건만으로도 충분하기 때문에 디리클레 조건만 확인해도 문제가 없다.
$$ \int_{-\infty}^{\infty}|f(x)|dx < \infty $$
절대적분가능 조건
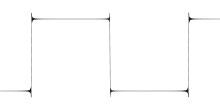
깁스 현상 (Gibbs Phenomenon)
Piecewise Smooth 함수에도 푸리에 시리즈의 부분합 개념을 적용할 수 있지만 불연속점에서 깁스 현상이 발생할 수 있다는 점을 기억해야 한다. 깁스 현상이란 불연속점에서 푸리에 합의 오버슛이 발생하는 현상을 말한다. 깁스 현상을 최소화하기 위해서는 불연속점을 중간값으로 보간할 수 있는 필터를 적용하면 최소화시킬 수 있다.