z 변환
작성일 : 2023년 03월 12일 (Sunday)
Table of contents
z 변환
z 변환은 이산시간 푸리에 변환을 모든 함수에 대해서 사용할 수 있도록 일반화한 변환이다.
$$ X(z) = \mathcal{Z} \{ x[n] \} = \sum_{n=-\infty}^{\infty}{x[n]z^{-n}} $$
$$ x[n] = \mathcal{Z}^{-1}\{ X(z) \} = \frac{1}{2\pi j}\oint_{C}{X(z)z^{n-1}dz} $$
z 변환
일반화했다는 것은 더 넓은 범위에서 사용할 수 있다는 것이다. DTFT가 $X\left ( e^{jw} \right )$로 표현되는 이유는 z변환에 $z = e^{jw}$ 를 넣은 형태이기 때문이다. z변환에서는 $z = re^{jw}$ 이고 DTFT는 z변환에서 r이 1인 형태를 말한다. z변환은 극점의 위치로 시스템의 안정성을 판단할 수 있고, 시스템의 인과성과 안전성을 결정하는 정보를 얻을 수 있으며 복잡한 컨볼루션을 쌍대성을 사용해서 간단한 곱셈의 형태로 풀어낼 수 있기 때문에 사용된다. 주파수 분석을 위한 용도가 아니기 때문에 푸리에 변환/시리즈와는 결이 조금 다르다는 것을 알 수 있다.
ROC (Region of convergence)
z변환에 사용된 r의 용도는 무엇일까? z변환식에 $re^{jw}$ 적용하게 되면 DTFT 대비 $r^{-n}$ 이 추가되어 감쇠효과를 주게된다. 즉, DTFT를 사용할 때 함수가 유한한 에너지를 가지도록 디리클레 조건을 만족해야 했는데 z변환에서는 식자체에서 감쇠를 적용하기 때문에 DTFT보다 넓은 수렴범위를 갖게된다는 것이다. DTFT는 안되는데 Z변환은 되는 간단한 함수는 단위계단함수이다. 단위계단함수는 디리클레 조건을 만족시키지 못하기 때문에 DTFT가 없지만, 1보다 큰 r에 대해서는 z변환이 존재한다. 즉, ROC란 DTFT는 없는데 특정범위에서는 z변환이 가능하다는 것을 표현하기 위한 범위라고 볼 수 있다. 다음과 같은 그림으로 ROC가 그려진다. 즉, r의 크기로 ROC가 표현된다고 보면된다.
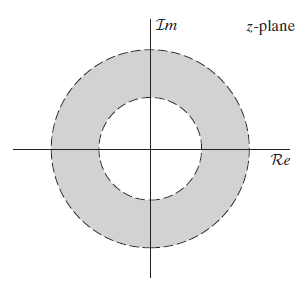

ROC가 r=1을 포함하면 DTFT 역시 존재한다고 보면된다.


사용법
z 변환은 $X(z) = \frac{P(z)}{Q(z)}$ 와 같은 형태의 식을 분석할 때 아주 용이하다. (주로 전달함수) P(z)의 근을 영점, Q(z)의 근을 극점이라고 하는데 이 영점, 극점, ROC의 배치에 따라 안정도를 평가할 수 있다. 이와 관련해서는 자동제어를 참고하자.
</figure>
–>