기계학과 전기역학
작성일 : 2023년 12월 02일 (Saturday)
Table of contents
우리가 빛이 무엇인지에 대해서 제대로 이해하기 시작한 역사는 그리 오래되지 않았다. 빛은 무엇일까? 전자기학에서 빛을 논해야 하는 이유에 대해서 아래 내용을 살펴보자.
뉴턴의 고전 역학 (17세기 말)
기계학은 17세기 말 뉴턴의 고전 기계학으로부터 시작했다. 그 유명한 뉴턴의 운동법칙인 제1법칙 관성의 법칙, 제2법칙 가속도의 법칙, 제3법칙 작용반작용의 법칙이다. 제1법칙의 관성력은 영어로 Inertial Force 이라고 한다. 뉴턴의 운동법칙에 따르면 관성력은 힘이라고 분류하기는 애매해서 겉보기힘, 가짜힘이라고도 불리는데, 대표적인 예시가 원심력과 전향력이다. 관성력은 비관성좌표계(가속좌표계)에서만 유효하고, 관성좌표계에서는 항상 0이다.
관성좌표계와 비관성좌표계(가속좌표계) 관성좌표계는 정지 또는 등속운동에 대한 좌표계이고, 비관성좌표계는 가속/감속운동에 대한 좌표계이다. 즉, 관성좌표계는 ‘가속도 = 0’에 대한 좌표계이고, 비관성좌표계는 ‘가속도 ≠ 0’에 대한 내용이다.
만유인력의 법칙
뉴턴은 중력을 설명하기 위해서 서로 다른 물질들은 서로 끌어 당기는 힘이 있다고 가정했다. 이게 만유인력의 법칙인데, 공식은 다음과 같다.
$$ F = \frac{Gm_1m_2}{r^2}\overrightarrow{e_r} $$
만유인력의 법칙 (inverse-square law)
$m_1$, $m_2$의 질량을 가진 두 물질은 두 물질 간의 거리인 r의 제곱에 비례하고 그 크기는 중력상수(혹은 뉴턴상수) G에 비례한다는 것이다. $\overrightarrow{e_r}$은 힘의 방향을 가리킨다. 이 힘이 질량이 m인 물질에 가해지면 가속도 a를 얻는다는 가설이다.
푸아송 방정식 (19세기 초)
푸아송은 라플라시안 연산자와 선속, 그리고 소스를 이용해서 선속과 소스(source)의 관계를 표현하였다. 식으로 표현하면 다음과 같다.
$$ \nabla ^2 \Phi = \sigma (x) $$
푸아송 방정식 (Poisson's Equation)
위는 일반적인 공식이다. 우리는 앞으로 정전계, 정자계를 다룰 것이기 때문에 소스가 0이라고 가정할 것이다. 이게 바로 라플라스 방정식이다. 라플라스 방정식은 정전계, 정자계를 풀어나가는 데 있어서 핵심적인 공식이 될 것이다. 소스가 0이라는 이야기는 역학적으로 풀어내자면 관성계를 의미할 수 있겠다. 관성계에 대해서 알고싶다면 내 블로그에서 검색해보자.
맥스웰 방정식 (19세기 말, 1865년)
19세기 말 맥스웰은 정전계와 정자계에 대한 4가지의 방정식을 세웠다. 각 방정식은 일단 다음과 같다.
$$ \nabla \cdot E = \frac{\rho}{\epsilon} = \Phi \tag{1} $$
$$ \oint _S \overrightarrow{E} \cdot d\overrightarrow{a} = \frac{\rho}{\epsilon} = \Phi \tag{1-1} $$
$$ \nabla \cdot B = 0 \tag{2} $$
$$ \oint _S \overrightarrow{B} \cdot d\overrightarrow{a} = 0 \tag{2-1} $$
$$ \nabla \times E = -\frac{\partial B}{\partial t} \tag{3} $$
$$ \nabla \times B = \mu J + \mu\epsilon\frac{\partial E}{\partial t} \tag{4} $$
맥스웰 방정식 (Maxwell's Equation) in Introduction to Electrodynamics 7.3.3 by David J. Griffiths
(1) 방정식 : 전기장에 대한 가우스 법칙 (미분형)
(1-1) 방정식 : 전기장에 대한 가우스 법칙 (적분형)
(2) 방정식 : 자기장에 대한 가우스 법칙 (미분형)
(2-1) 방정식 : 자기장에 대한 가우스 법칙 (적분형)
(3) 방정식 : 패러데이의 법칙
(4) 방정식 : 암페어 주회 법칙 (w/Mawell’s correction)
전기장에 대한 가우스의 법칙은 전기장의 발산은 내부 전하에 비례한다는 의미이다. 또, 총 전속($\Phi$)은 $\frac{\rho}{\epsilon}$와 같다.
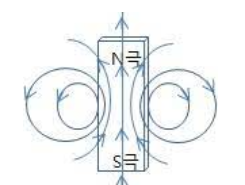
자기장에 대한 가우스의 법칙이 의미하는 바는 자속은 단순히 발산하지 않고 시작점으로 다시 돌아온다는 의미이다. 자기력선은 시작과 끝점이 동일하므로 폐 곡면에 대한 총 자속은 0이 된다. (서로 상쇄)

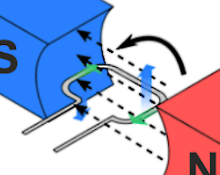
패러데이의 법칙은 맥스웰의 법칙이 아니더라도 흔히 들었을만한 법칙이다. 면적 S에 대해 자속이 변하면, 면적 S의 경계라인에 e.m.f(electromotive force)가 생성된다는 것이다. 패러데이의 법칙에서 부호 -는 렌츠의 법칙에 따른 것이다.
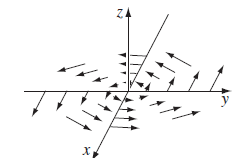
암페어 주회 법칙은 전류가 흐르는 물질의 주변에서는 자기장이 발생한다는 것이다. 자기장의 방향은 오른 나사의 법칙을 따른다.
이 푸아송 방정식과 맥스웰의 법칙을 이용하면 최종적으로 다음과 같은 식이 얻어진다.
$$ \nabla \cdot g = -4\pi G\rho $$
$$ \nabla ^2 \Phi = \nabla \cdot (\nabla \Phi) = 4\pi G\rho $$
푸아송 방정식 형태로 나타낸 중력포텐셜
광전효과 (19세기 말)
독일의 물리학자 하인리히 루돌프 헤르츠는 진공 상태의 금속판에 빛을 비추면 무언가 튀어나온다는 사실을 발견했고, 곧 영국의 물리학자 조지프 톰슨이 그 것이 전자라는 것을 밝혀 냈다. 하지만, 모든 색의 빛이 광전현상을 나타내는 것은 아니었다. 당대에는 이 현상이 의미하는 바를 완벽하게 해석하지 못했다.
광전효과의 해석에 앞서서 먼저, 빛과 관련된 연구를 돌아보자. 17세기 뉴턴은 프리즘을 통과한 빛의 한 줄기를 다시 프리즘으로 통과시켜도 더 이상 분해되지 않는다는 것을 발견했고, 빛은 입자라는 결론을 지었다. 하지만, 18세기 말 토머스 영의 이중 슬릿 간섭 실험을 통해 빛이 파동성을 지닌다는 것이 증명되며 빛은 파동이라는 가설이 유력해졌다. 이후 19세기 말 맥스웰이 전기장과 자기장이 합쳐지면 전자기파가 만들어질 수 있고, 이 전자기파의 속도가 이론적으로 빛의 속도와 거의 일치한다는 것을 밝혀내며 빛 또한 일종의 전자기파라는 가설을 세웠고, 빛은 파동이라는 쪽에 힘을 더 실어주었다.
하지만, 1899년 플랑크 상수 발표 이후, 빛이 단순 파동이라는 가설이 흔들리기 시작했다. 과거 흑체(열을 완전히 흡수해서 전자기파를 방출하거나, 전자기파를 완전히 흡수하는 물체)라는 물질을 가정하여 흑체 복사실험을 진행했다. 열을 가하면, 흑체에서 전자기파가 방출되면서 색이 관찰되었다. 온도가 높아질 수록 파장이 점점 짧아진다는 것이 관찰되었다. 이 현상의 데이터를 회귀분석하여 빈, 레일리, 플랑크가 각자의 공식을 발표했는데 그 중 플랑크의 공식이 가장 잘 맞아떨어진다.
플랑크는 흑체는 진동하는 입자인 진동자로 이루어져 있고, 진동자는 진동수에 비례하는 에너지 덩어리인 복사에너지를 흡수할 수 밖에 없음을 발견했고, 흑체 복사에 대한 빈의 공식을 일부 개선하여 흑체 방출 결과와 거의 동일한 공식을 유도하였다. 결과적으로 $E = nhv = \hbar v$의 공식을 얻었고($h = 6.62607015 \times 10^{−34}$J⋅s), 빛의 에너지는 주파수에 따라 양자화되어 있고, 결론적으로 에너지가 주파수에 비례한다는 양자가설을 세웠다. 고전역학에서 모든 에너지는 연속적이기에 플랑크의 주장은 당대의 상식을 뒤엎는 획기적인 내용이었다.
이후, 위 내용을 바탕으로 1905년 아인슈타인은 빛 역시 입자(광양자 혹은 광자로 불림)로 이루어져있다는 광양자 가설을 냈다. 이를 통해 빛은 파동성도 가지고 있지만 입자성도 가지고 있다고 하는 것이 현재까지도 가장 신빙성이 높은 가설이다. (즉, 거의 기정사실화되어 있는 내용이다.)
상대성이론 (20세기 초)
고전 역학만으로는 아주 빠른 속도(Ex: 빛의 속도)로 운동하는 현상을 다룰 수가 없었다. (Ex: 19세기에 진행된 마이컬슨-몰리 실험) 따라서, 20세기 초 아인슈타인은 시간과 공간에 대해 기존의 잘못된 관념을 전환시킨 상대성 이론(theory of relativity)을 발표하였다. 이 상대성이론은 고전역학의 상대성 이론을 완전히 대체하였다.
상대성이론은 일반 상대성(GR; general Relativity)이론과 특수 상대성(SR; Special Relativity)이론이 있다. 여기서, 우리는 특수 상대성 이론만 다룬다. 일반 상대성 이론은 고전역학의 만유인력을 대체하여 현대 물리학에서 가장 성공적인 중력 이론이라는 정도만 남겨둔다.
특수상대성 이론 (1905)
아인슈타인은 광속 불변의 법칙을 세워서, 기존의 갈릴레이의 상대성 원리가 전자기학에서도 성립함을 증명했다. 상대성 원리는 뉴턴의 고전역학에서도 쓰고 있던 개념으로 관성계에서는 같은 물리법칙이 적용된다는 것이고, 광속 불변의 법칙은 모든 관성계에서는 빛의 속도가 일정하다는 것이다.
특수 상대성 이론의 증명 상대성 원리와 광속 불변의 법칙을 기준으로 맥스웰 방정식을 수정하면 모든 관성계에서 빛의 속도가 일정하다는 내용이 증명된다. 이 증명을 통해 맥스웰 공식의 유효성을 또 다시 증명해보였고, 빛이 전자기파라는 가설에도 더 힘을 실어주어 아직까지도 빛은 전자기파라고 우리는 배우고 있다.
광속 불변의 법칙은 가설에 불과했지만, 이후 드 지터의 쌍성 실험이 광속은 항상 일정하다는 쪽에 힘을 더 실어주었다. 고전물리학 관점에서 아래와 같이 행성이 공전해서 지구와 가까워지는 방향으로 이동할 때는 빛의 속도가 느려졌다가, 멀어질 때는 빛의 속도가 느려져야 하는데 실제로는 그렇지 않다는 것이다.
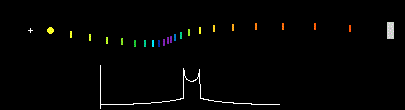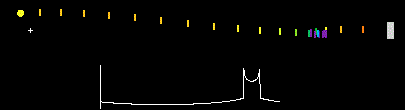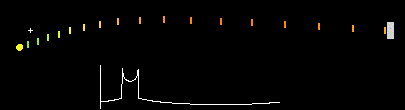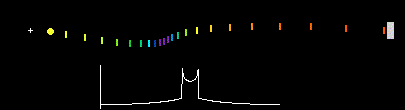

특수상대성 이론의 결론
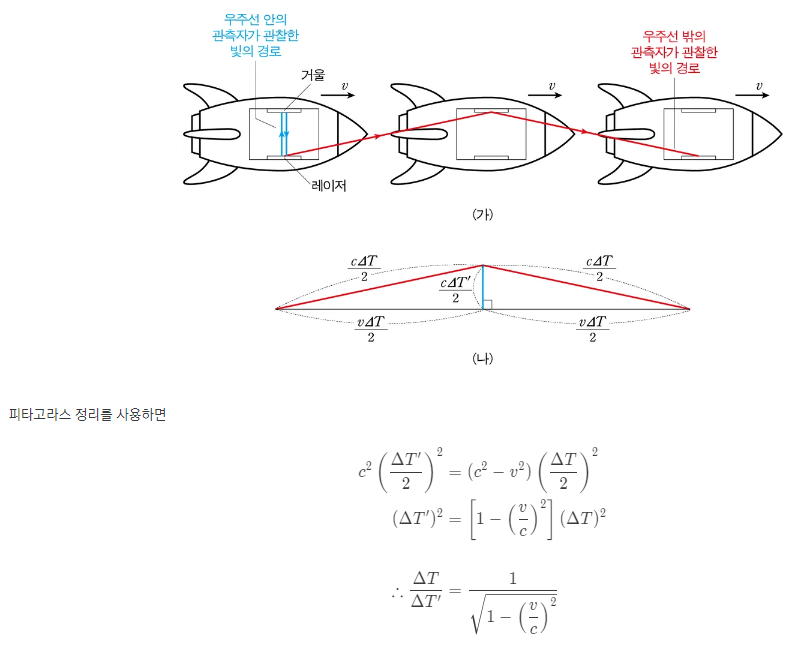
특수 상대성 이론의 중요한 결론은 빠른 운동에 의해서 시간팽창, 길이수축이 일어날 수 있다는 점이다. 시간팽창은 빠르게 움직이는 관성계는 시간이 느리게 간다는 것이고, 길이수축은 빠르게 움직이는 관성계는 이동하는 방향축의 길이가 짧아진다는 것이다.
시간 팽창 가설에 따르면 과거 고전역학에서는 우주 어디서든 시간의 진행방식이 같아서 같은 속도로 흘러간다고 해서 ‘절대시간’이라고 칭했지만, 시간 팽창 가설에 의하면 운동하는 시계의 진행은 느려지고, 그 속도가 빛의 속도와 동일해지면 시간이 멈춘다라는 가설을 내세웠다.
그리고 길이수축에 대해 이야기하자면 광속 불변의 법칙에 따라 길이가 수축된다. 로렌츠 변환에 의해서 고유길이 $L’$은 $L$로 변환된다. 아래 변환식에서 $\gamma$는 로렌츠 인자이다. 자세한 내용은 아래의 식과 그림을 참고하자.
$$ L = L'\sqrt(1 - (\frac{v}{c})^2) = \frac{L'}{\gamma} $$
로렌츠 변환

- 참조문헌
- Spacetime and Geomery (by. Sean Carroll)
- Introduction to Electrodynamics (by. David J. Griffiths)
- 참조 글