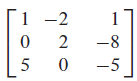벡터와 행렬
작성일 : 2023년 02월 01일 (Wednesday)
Table of contents
벡터는 열의 크기가 1인 행렬을 말한다. 벡터를 사용하면 행렬로 표현된 여러 개의 방정식을 하나의 방정식처럼 나타낼 수 있다.
벡터 방정식
$$ 4x_{1} + 5x_{2} = 3 $$
$$ 5x_{1} = 5 $$
벡터를 이용하면 계수를 아래와 같이 표현할 수 있다.
$$ \mathbb{\textbf{u}} = \begin{bmatrix}4 \\ 5\end{bmatrix} \mathbb{\textbf{v}} = \begin{bmatrix}5 \\ 0\end{bmatrix} \mathbb{\textbf{w}} = \begin{bmatrix}3 \\ 5\end{bmatrix} $$
방정식을 벡터를 사용해서 다시 정리하면 아래와 같다.
$$ \mathbb{\textbf{u}} x_{1} + \boldsymbol{\mathbb{\textbf{v}}} x_2 = \boldsymbol{\mathbb{\textbf{w}}} $$
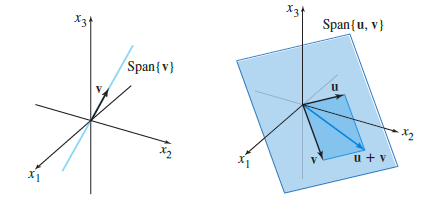
Span
벡터에 스칼라를 곱해서 얻어지는 모든 벡터의 조합을 Span이라고 한다. 벡터 $\mathbb{\textbf{u}}$, $\mathbb{\textbf{v}}$가 정의되어 있다고 가정하면, Span{$\mathbb{\textbf{u}}$}, Span{$\mathbb{\textbf{u}}, \mathbb{\textbf{v}}$}는 아래와 같다.

행렬 방정식
벡터 방정식에서 들었던 예시를 다시 그대로 가져와서 사용해보자. 계수 벡터를 $\mathbb{\textbf{u}}$, $\mathbb{\textbf{v}}$를 행렬로 합치고, 변수를 하나의 벡터로 만들면 완전한 방정식으로 표현할 수 있다.
$$ 4x_{1} + 5x_{2} = 3 $$
$$ 5x_{1} = 5 $$
$$ \mathbb{\textbf{A}} = \begin{bmatrix}4 & 5 \\ 5 & 0\end{bmatrix} \mathbb{\textbf{x}} = \begin{bmatrix}x_{1} \\ x_{2} \end{bmatrix} \mathbb{\textbf{w}} = \begin{bmatrix}3 \\ 5\end{bmatrix} $$
$$ \mathbb{\textbf{A}}\mathbb{\textbf{x}} = \boldsymbol{\mathbb{\textbf{w}}} $$
특성
행렬 방정식은 분배법칙, 교환법칙이 성립한다.
- 분배법칙 : $A(\mathbb{\textbf{u}}+\mathbb{\textbf{v}}) = A\mathbb{\textbf{u}} + A\mathbb{\textbf{v}}$
- 교환법칙 : $A(c\mathbb{\textbf{u}}) = c(A\mathbb{\textbf{u}})$
해의 종류
동차 선형시스템 (Homogeneous Linear System)
$\mathbb{\textbf{A}}\mathbb{\textbf{x}} = \mathbb{\textbf{0}}$ 의 형태로 표현할 수 있는 선형시스템을 동차 선형시스템이라고 한다. 동차 선형시스템은 항상 $\mathbb{\textbf{x}} = \mathbb{\textbf{0}}$의 자명해(trivial solution)를 갖는데, 이 해는 시스템을 분석하는 데 있어서 보통 의미가 없는 해이다. 따라서, 비자명해(nontrivial solution)을 찾는게 중요하다. 비자명해는 적어도 하나 이상의 자유변수가 있을 때에만 존재한다.
비동차 선형시스템 (Nonhomogeneous Linear System)
동차 선형시스템 식으로 표현할 수 없고, $\mathbb{\textbf{A}}\mathbb{\textbf{x}} = \mathbb{\textbf{b}}$ 의 형태로 표현할 수 있는 선형시스템을 비동차 선형시스템이라고 한다. 비동차 선형시스템이 여러 개의 해를 가질 경우, 그 해는 매개변수 벡터 다항식의 형태로 표현된다. 만약, 아래와 같은 시스템이 있다고 가정해보자.
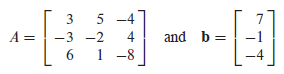
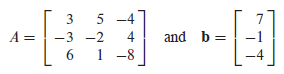
위와 같은 시스템을 사디리꼴 형태로 정리하고, 자유변수인 $x_{3}$를 기준으로 재정리하면 아래와 같은 형태로 정리된다.
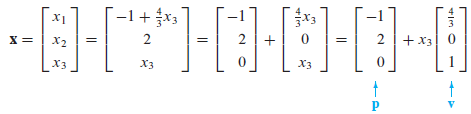
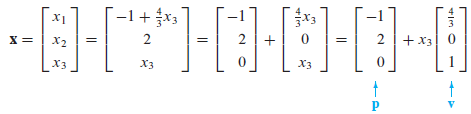
위와 같은 매개변수 벡터 다항식의 형태에서 $x_{3}$를 $t$로 일반화하면 $\mathbb{\textbf{x}} = \mathbb{\textbf{p}} + t\mathbb{\textbf{v}}$가 얻어진다.
그림으로 나타내면 아래와 같다.
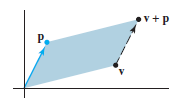

$t \in \mathbb{R}$이라는 것을 생각하여 $t\mathbb{\textbf{v}}$를 선분 L로 표시하면 아래와 같은 형태의 선으로 표현할 수 있다.
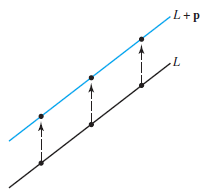

$\mathbb{\textbf{x}}=\mathbb{\textbf{p}}$는 $\textbf{A}\mathbb{\textbf{x}} = \mathbb{\textbf{b}}$을 만족하기 위한 최소한의 해이다($t = 0$ 일때의 해). $t\mathbb{\textbf{v}}$의 궤적 L에 $\mathbb{\textbf{p}}$를 더해서 최종적으로 $\mathbb{\textbf{x}}=\mathbb{\textbf{p}}+t\mathbb{\textbf{v}}$의 형태로 표현된다.