DSP 관련 기초 지식
작성일 : 2023년 03월 06일 (Monday)
Table of contents
복소 정현파
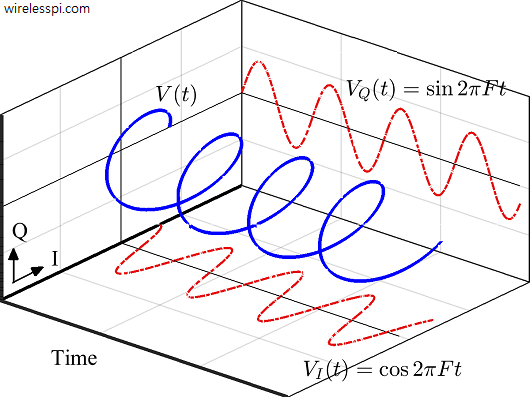
복소 정현파는 사인함수와 코사인함수를 각각 실수축, 허수축에 매칭해서 복소수 평면(극 좌표계)에 표현한 정현파를 의미한다. 복소 정현파를 극좌표로 표현한 것이 페이저이다.

오일러 공식
스위스 바젤 출신 수학자 오일러가 발견한 공식이다. 오일러 공식을 이용하면 복소 정현파를 자연수 e의 지수함수 형태로 변경하여 주파수가 다른 정현파 간 곱셈이나 나눗셈을 쉽게 할 수 있다.
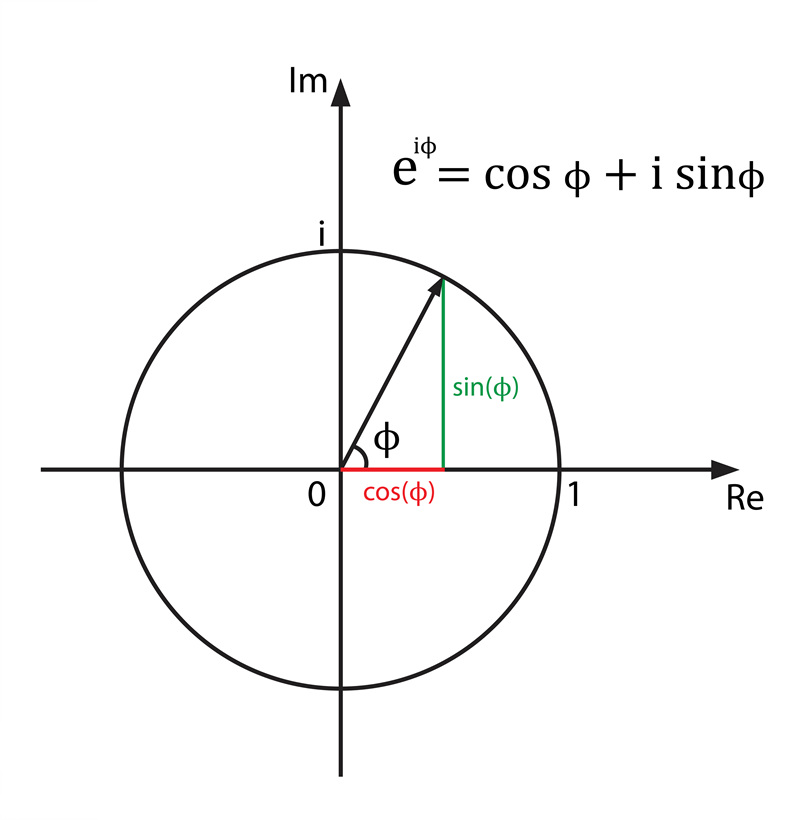

$$ e^{j\theta} = \cos{x} + j\sin{x} $$
$$ \cos(\theta) = \frac{\exp(j\theta)+\exp(-j\theta)}{2} $$
$$ \sin(\theta) = \frac{\exp(j\theta)-\exp(-j\theta)}{2j} $$
LTI (Linear Time Invariant) or LSI (Linear Sample Invariant)
특정 함수에 입력을 넣었을 때 출력이 항상 일정한 시스템을 연속시간에 대해서는 LTI 시스템, 이산시간에 대해서는 LSI 시스템이라고 말한다. 이러한 시스템들은 보통 이전의 출력이 중첩되고(Memory), 특정 입력에 대한 출력이 일정하고(Time Invariance), 선형성(Linearity)을 가지고 있다. 아래는 LTI 시스템에 대한 전반적인 영상 설명이다.
- 0m 00s ~ 1m 36s : LTI 시스템이란?
- 1m 36s ~ 2m 31s : 단위 임펄스와 단위 임펄스 응답
- 2m 32 ~ : 임펄스 응답 (LTI 시스템 전달함수)
컨볼루션 (합성곱, Convolution)
컨볼루션은 합성곱이라는 뜻으로 LTI 시스템의 분석에 사용된다. 컨볼루션을 사용하면 두 함수의 연관성을 확인할 수 있다. 컨볼루션은 아래 연속시간 컨볼루션 예시 1에서 볼 수 있듯 $g(t)$를 $g(t - \tau)$로 표현하여 $\tau$만큼 평행이동한 $g$가 $f$의 곱셈을 $-\infty \sim \infty$ 범위안에서 더하는 것이다.
$$ 연속시간 : (f * g)(t) = \int_{-\infty}^{\infty}f(\tau)g(t-\tau)d\tau $$
$$ 이산시간 : (f * g)[n] = \sum_{m=-\infty}^{\infty}f[m]g[n-m] $$
컨볼루션 공식
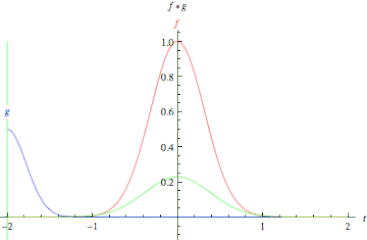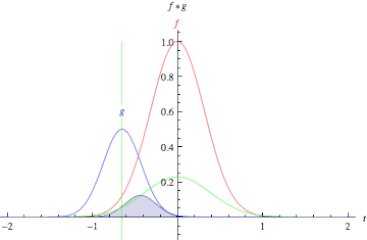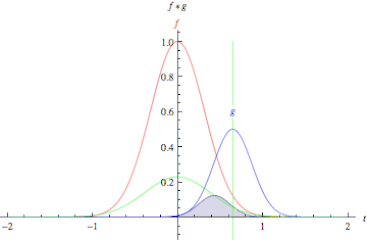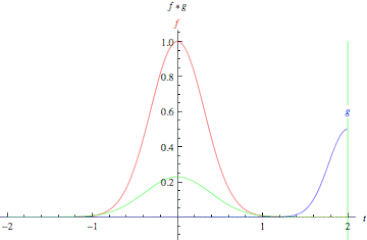

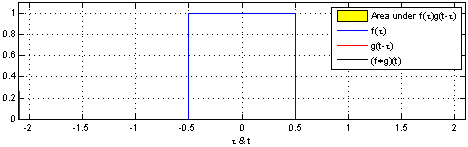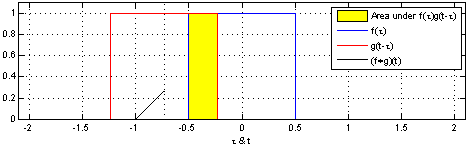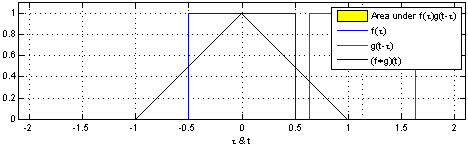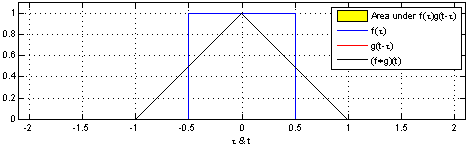

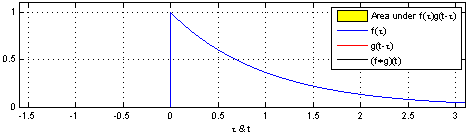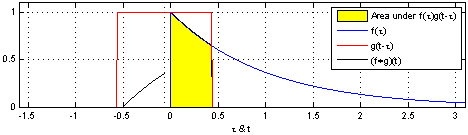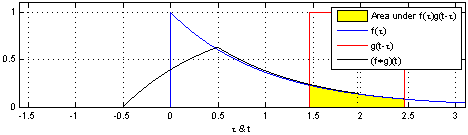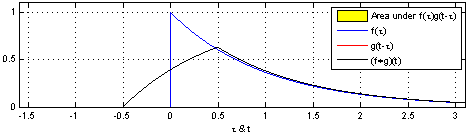

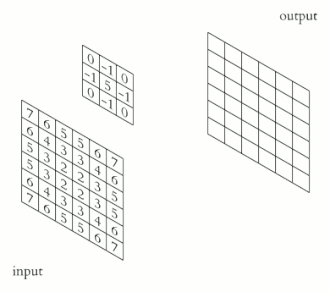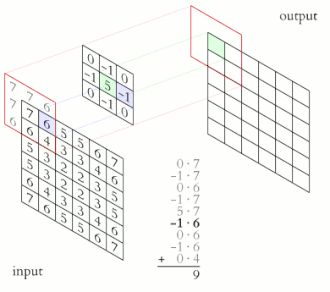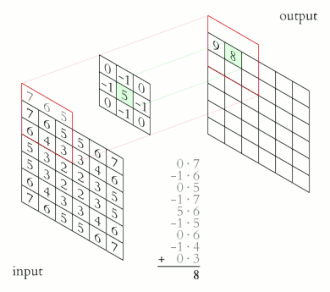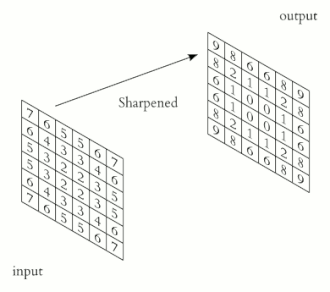

컨볼루션의 성질
컨볼루션은 이산시간, 연속시간에 대하여 교환법칙, 결합법칙, 분배법칙이 성립한다.
임펄스 응답 $h[n]$
임펄스 응답이란 시스템에 무한한 임펄스 함수(impulse train)를 입력했을 때의 응답을 말한다. 임펄스 응답을 사용하여 시스템의 응답 특성(전달 함수)을 알 수 있다. 임펄스 응답을 인가하면 위 연속시간 컨볼루션 gif를 참고해보면, 임펄스 응답을 모든 n마다 보내고 있다고 생각하면 된다. 물론, 위 예시는 4번째 gif를 제외하고는 모두 연속시간이므로 완벽하게 같지는 않지만 샘플링된 신호가 이동한다고 생각해보면 도움이 될 것이다.
LTI 시스템의 전달함수
LTI 시스템에 대한 임펄스 응답은 LTI 시스템의 전달함수와 같다.
$$ y[n] = \sum_{k=-\infty}^{\infty}{x[k]h[n-k]} $$
LTI 시스템 전달함수 (임펄스 응답)
함수의 내적
함수의 내적은 두 함수 간의 연관성 (Correlation) 검사에 사용된다. 식은 아래와 같다.
$$ \lt f(t), g(t) \gt = \int_{a}^{b}f(t)g^*(t) dt $$
연속시간에서의 함수의 내적
$$ \sum_{n=0}^{N-1}{f[n]g^*[n]} $$
이산시간에서의 함수의 내적
시스템의 특징
시스템은 MemoryLess (무기억) / Linear (선형) / Time-Invarint (시간불변) / Causal (인과적) / Stable (안정적인) 의 특성을 가질 수 있다. 각각 설명하면, 무기억은 현재의 값만으로 출력이 결정되는 성질, 선형은 출력이 입력에 대해 선형적인 관계를 가진다고 할 때를 말하고, 시간불변은 시스템에 동일한 입력을 넣으면 언제든지 동일한 출력을 가진다는 것을 말하고, 인과적이라는 것은 출력이 이전의 입력과 현재값만을 기준으로 결정된다는 것이고, 안정적이라는 것은 입력이 유한하다면 출력도 유한한 것을 말한다.