벡터 대수학
작성일 : 2023년 04월 19일 (Wednesday)
Table of contents
벡터 연산의 의미를 기하학적으로 잘 이해하는 것은 중요하다.
덧셈/뺄셈
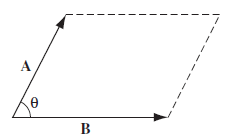
벡터를 더하거나 뺀다는 것은 두 벡터의 시점과 종점을 하나로 통합하는 과정이다. 아래의 그림을 참고하자. 덧셈에 대해 교환법칙/결합법칙/분배법칙이 성립한다.
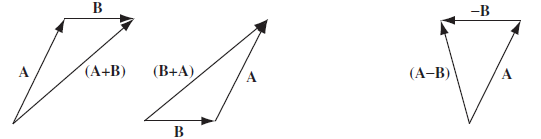

$$ A + B = B + A $$
$$ (A + B) + C = A + (B + C) $$
$$ a(A + B) = aA + aB $$
내적 (dot product, scalar product)
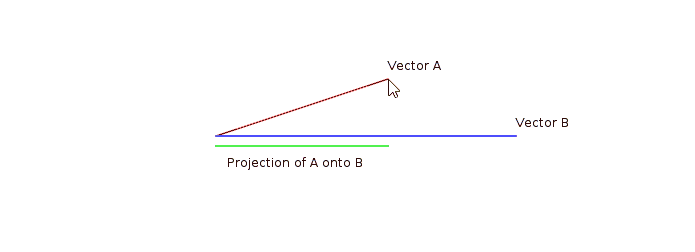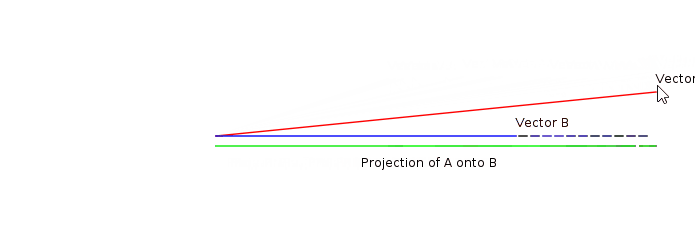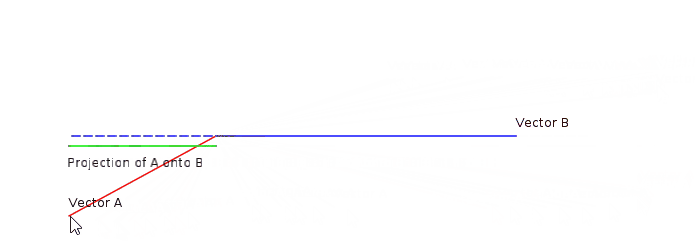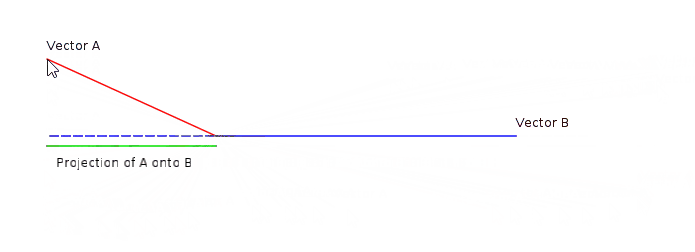
내적은 두 벡터가 얼만큼 닮아 있는지 판별할 수 있는 척도이다. 두 벡터의 내적은 두 벡터가 선형 종속인 관계에 있을 때 그 절대값이 가장 크다. (즉, $\theta$가 0이거나 $\pi$인 경우)
$$ A \cdot B = \left\lVert A \right\rVert \left\lVert B \right\rVert \cos{\theta} $$
두 벡터 중 하나의 벡터를 고정시키고, 다른 벡터를 원점에 대해서 회전시키면 그 의미를 더 명확하게 알 수 있다.

외적 (cross product)
외적은 토크 계산시 굉장히 유용하다. 외적의 크기는 두 벡터가 만드는 평행사변형의 크기와 동일하다.
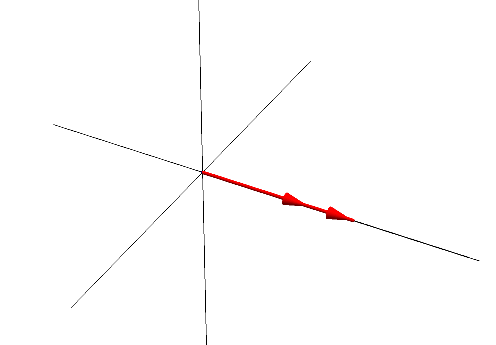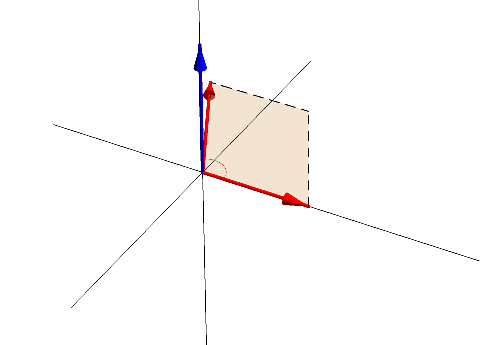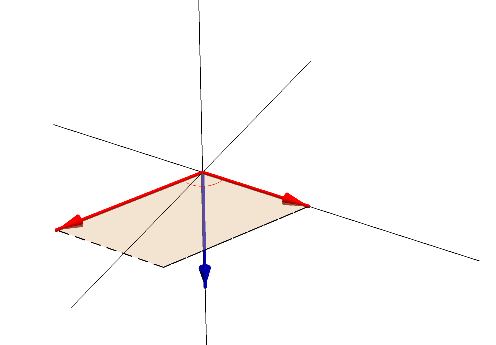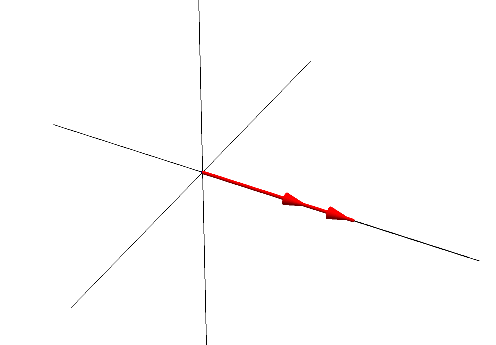


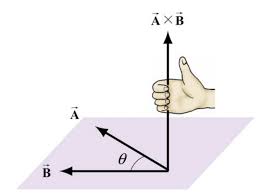
외적의 방향은 오른손 법칙을 이용하여 결정할 수 있다. 축을 중심으로 오른손을 A에서 B로 감쌀 때 엄지의 방향이 외적의 방향이다. B에서 A로 감싼다면 엄지의 방향은 아래를 향할 것이다. 즉, 외적에 대한 교환법칙은 성립하지 않는다. 단, 분배법칙은 성립한다.

유용한 연산(증명)
외적과 내적을 이용해서 여러가지 유용한 벡터 연산식을 만들어 낼 수 있다. 증명은 사실 좀 활용도에 비해서 과한 부분이 없지 않아서, 내용만 다룬다.
스칼라 삼중곱 (Scalar Triple Product)
스칼라 삼중곱은 3개의 벡터를 곱했을 때 스칼라 값이 얻어지는 연산이다. 연산식은 다음과 같다. 재밌는 점은 스칼라 삼중곱은 순서가 상관이 없다.
$$ \left[ ABC \right] = A \cdot (B \times C) = A \land B \land C $$
스칼라 삼중곱은 평행 6면체의 부피와 동일하다.
벡터 삼중곱 (Vector Triple Product; BAC-CAB 룰)
벡터 삼중곱 공식은 아래와 같다.
$$ A \times (B \times C) = B(A \cdot C) - C(A \cdot B) $$