벡터공간와 부분공간
작성일 : 2023년 02월 05일 (Sunday)
Table of contents
벡터 공간 (Vector Space)
벡터 공간이란 벡터가 만들어 낸 공간을 말한다. 벡터공간은 간단하게 말하자면 우리가 앞서 다룬 벡터의 연산 규칙, 벡터의 개념을 만족하는 공간이라고 보면 된다. 동일 벡터공간에 포함된 벡터들끼리는 아래의 연산을 모두 만족해야 한다.


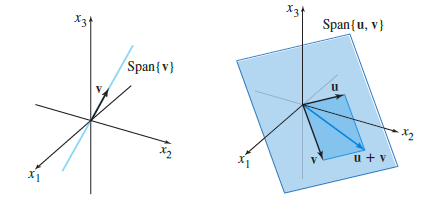
만약 벡터 공간 $\textbf{V}$를 $\textbf{u}$, $\textbf{v}$로 표현할 수 있다고 가정해보자. 벡터 공간을 정의할 수 있는 최소한의 선형독립적인 벡터의 집합을 기저(basis)라고 한다. 보통 $\beta$로 표현된다.
부분 공간 (Subspace)
부분 공간이란 벡터 공간의 특성을 만족하는 특정 벡터 공간의 부분집합을 의미한다. 가장 대표적인 예시로 3차원 직교좌표계($x_{1}$축, $x_{2}$축, $x_{3}$축)이 있다고 할 때, $x_{1}$-$x_{2}$평면이 부분집합이다. 한 마디로 정리하면, $v_{1}$, $v_{2}$, … , $v_{p}$가 벡터 공간 $\textbf{V}$에 있는 선형독립 벡터라면, Span{$v_{1}$, $v_{2}$, … , $v_{p}$}이 벡터 공간 $\textbf{V}$의 부분 공간이다.
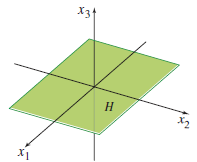

부분 공간의 차원은 원 벡터 공간의 차원을 넘을 수 없다. (즉, 같거나 작다.)
선형변환 ($ x \mapsto Tx$)
적분변환은 특정 좌표계에서 정의된 함수를 적분을 통해 또 다른 좌표계로 맵핑하는 작업을 말한다. 특정 벡터 공간($\mathbb{\textbf{R}}^n$)에 T(n x m)를 곱하면, 또 다른 벡터 공간 ($\mathbb{\textbf{R}}^m$) 으로 맵핑된다.
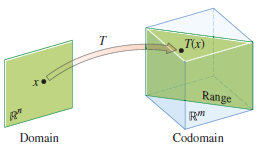

Kernel (Null Space)
커널은 선형변환에서 특정 공간에서 다른 공간으로 변환해주는 벡터를 말한다.
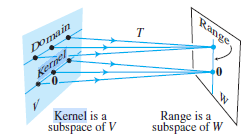

영공간 (Null Space)
행렬 $\textbf{A}$가 존재할 때, $\textbf{A}\textbf{x}=0$ 을 만족하는 벡터 $\textbf{x}$가 만든 벡터 공간을 영공간이라 한다.
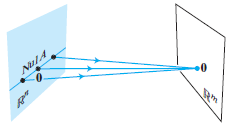

열공간 (Column Space)
열공간은 Span{$v_{1}$, $v_{2}$, … , $v_{p}$}을 부분공간으로써 표현한 말이다. 행렬 $\textbf{A}$에서 열들을 각각 하나의 벡터로 사용해서 얻은 벡터공간을 말한다.
행공간 (Row Space)
행렬 $\textbf{A}$에서 행들을 각각 하나의 벡터로 사용해서 얻은 벡터공간을 말한다.
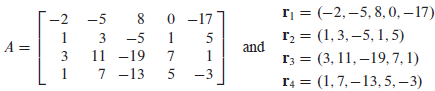
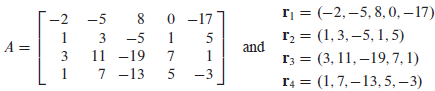
랭크 (Rank)
랭크는 행렬 $\textbf{A}$에 대한 열공간의 차원을 의미한다. 즉, 부분 공간의 차원을 의미한다. 랭크를 알면 여러가지 내용을 간단히 알 수 있다.