DFT 설명
작성일 : 2025년 05월 18일 (Sunday)
우리는 지금까지 CTFS/CTFT/DTFS/DTFT 를 살펴보며 주기함수와 비주기함수의 주파수 분석방법을 학습했다. 하지만, 앞서 다룬 내용들은 실제로 산업에서 사용하기는 어렵고 이론적인 분석 툴이었다. 이제 실제로 디지털 신호 처리에 사용되는 기술들을 중점적으로 살펴보자.
DFS (Discrete Fourier Series)
DFS와 DTFS는 동일하다. DFS는 $e^{-jw_{0}}$을 $W_{N}$ 으로 표시한다는 것 말고는 차이점이 존재하지 않는다. ($w_{0} = \frac{2\pi}{N}$)
DFT (Discrete Fourier Transform)
DFT는 DTFT를 주파수 영역에서 샘플링한 버전이다. 즉, DTFT 가 불가한 경우 DTFT 의 일부 주파수의 성분이라도 보겠다는 것이다. 식으로 보면 다음과 같다.
$$ \widetilde{X}[k] = X(e^{jw}) \vert _{w=(2\pi/N)k} = X(e^{j(2\pi/N)k}) = X(e^{jw_{0}k}) $$
DTFT에 w=(2π/N)k 대입시
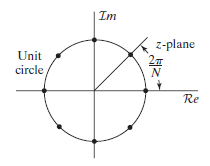
DTFT는 z변환의 단위원 위의 점들을 w주기로 표현한 것을 말하는 것이고, DFT는 단위원 위의 점들을 N개의 일정한 간격으로 샘플링한 것을 의미한다.

DFT를 식으로 정리하면 다음과 같다. DTFT와 별반 다르지 않다.
$$ \widetilde{X}[k] = \sum_{n = 0}^{N - 1} \widetilde{x}[n]W_{N}^{kn} $$
$$ \widetilde{x}[n] = \frac{1}{N}\sum_{k = 0}^{N - 1} \widetilde{X}[k]W_{N}^{-kn} $$
DTFT에 w=(2π/N)k 대입시
중요한 점은 0 ~ N-1 인 외의 k에 대해서는 X[k] = 0 이라는 것, 0 ~ N-1 외의 n에 대해서는 x[n] = 0 이라는 점이다. 즉, 바깥 범위는 고려하지 않는다. 이 얘기가 무슨 이야기이나면 DFT는 연속적인 데이터를 분석하는데 쓰이는 것이 아니고, 일시적인 유한한 데이터를 분석하는데 사용한다는 것이다. 샘플이 많아질수록 주파수 분해능이 높아지므로 더 정확한 분석을 위해서는 더 많은 데이터를 가지고 분석을 돌려야 하는데, 그렇게 되면 계산의 속도가 느려져서 (복잡도 O(N^2)) 효과적인 계산을 위해 FFT (고속 푸리에 변환, 복잡도 O(N logN)) 가 사용되고 FFT 를 위한 알고리즘은 쿨리-튜키, 소인수 알고리즘 등 다양하게 존재한다.
ZT/DFT 간의 관계
DFT는 Z변환의 z 평면상의 단위원(|z| = 1) 위에서 유한 개의 점으로 샘플링 한 것과 같다. 즉, DTFT가 존재하지 않더라도 z변환이 존재하는 범위 내에서는 그 값을 알 수 있다는 의미이다.