포워드 컨버터
작성일 : 2023년 09월 18일 (Monday)
Table of contents
이번 포스트에서는 강압이 가능한 절연형 컨버터인 포워드 컨버터를 다룬다. 이번 포스트에서도 마찬가지로 아래의 룰이 적용된다.
컨버터 기본 설계 Rule (인덕터 에너지 저장형)
R1. 인덕터에 흐르는 전류와 저항에 흐르는 전류와 크기가 같고, 연속적이다. 다른 말로 한 주기동안 인덕터에 걸리는 전압의 평균은 0이다.
R2. 커패시터에 걸린 전압과 저항에 걸린 전압과 크기가 같고, 연속적이다. 다른 말로 한 주기동안 커패시터로 인해 발생한 전하량의 평균은 0이다.
R3. 부하는 가변적이다. 즉, 부하는 고정값이 아니므로 최대값, 최소값을 고려하여 컨버터를 설계해야 한다. 하지만, 한 주기내에서 부하는 일정하다고 가정한다.
R4. 컨버터는 전원공급장치로 출력전압이 항상 정상범위 이내를 유지할 수 있도록 인덕터에는 적당한 에너지가 유지되어야 한다.
R5. MOSFET 게이트 드라이버의 스위칭 주파수가 높을 수록 컨버터를 더욱 컴팩트하게 설계할 수 있다. 하지만, 스위칭 주파수가 높다는 말은 게이트 드라이버가 고가라는 말이기도 하다.
R6. 인덕터 전류는 매 주기마다 일정한 값을 가진다. 이는 부하가 고정이라는 가정에 의한 것으로 실제로는 조금 차이가 날 수 있지만 주기가 매우 짧으므로 그 차이는 사실 미미(무시가능한 수준)하다. 즉, 도통 때 증가한 전류량과 차단 때 감소한 전류량은 거의 동일하다. ($| i_L(t) | \simeq | i_L(t + T)$ |)
R7. 출력전압이 일정하게 유지되기 위해서 커패시터는 적당히 큰 값으로 설정해야 한다. 즉, 시정수 (RC)를 고려해서 스위치가 OFF 되어도 커패시터 충전량만으로도 한 주기 동안은 커버가 될 정도가 되어야 한다. 이 내용에 대한 사양은 보통 출력전압 리플 요구사양으로 제시된다.
R8. 인덕턴스가 시스템에서 요구하는 사양 대비 과도하게 커지지 않도록 최소 출력저항이 얼마인지 고려하는 단계가 필요하다.
R9. 경부하모드를 제외하고는 인덕터 전류는 항상 0보다 큰 값을 유지할 수 있도록 하는 인덕턴스 값을 갖는 인덕터를 사용해야 한다.
개요
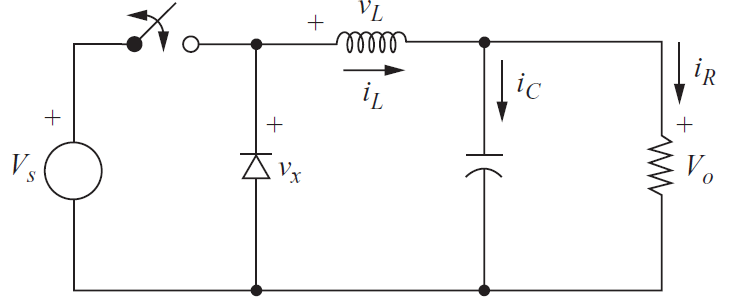
포워드 컨버터의 형태는 다음과 같다. 포워드 컨버터는 에너지를 전달하기 위한 1번 권선, 2번 권선이 있고 변압기의 자화 인덕터를 강제로 리셋시키기 위한 3번 권선이 존재한다. 리셋권선이 존재하는 이유는 플라이백과 다르게 자속이 반대방향으로 건너오지 않는다는 말을 의미하기도 한다. 이러한 동작 특성 때문에 포워드 컨버터라는 이름이 붙었다.
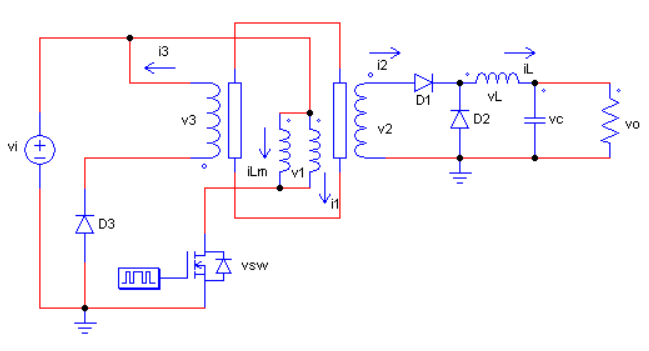

입출력 관계식은 위 Rule 6과 MOSFET OFF/SATURATION 시의 인덕터 전류를 비교하여 구할 수 있는데 과정은 다음과 같다.
$$ v_1 = V_S $$
$$ v_2 = v_1\frac{N_2}{N_1} = V_S\frac{N_2}{N_1} $$
$$ v_3 = v_1\frac{N_1}{N_3} $$
$$ v_L = v_2 - V_O = V_S\frac{N_2}{N_1} - V_O = L\frac{di_L}{dt} $$
$$ \frac{di_L}{dt} = \frac{V_S(N_2/N_1)-V_O}{L} = \frac{\Delta i_L}{DT} $$
$$ \therefore (\Delta{i_L})_{closed} = \left [ V_S\frac{N_2}{N_1} - V_O \right ] \frac{DT}{L} $$
한 주기 동안의 스위치 ON 때 인덕터 전류의 변화량
이 때, 스위치로 흐르는 전류는 $i_1 + i_{L_m}$이고, 자화 인덕턴스의 전류 변화량 $\Delta i_{L_m}$은 $\frac{V_SDT}{L_m}$이다.
한 주기의 도통시간(스위치 ON 시간)은 주기에 시비율을 곱한 값으로 위에서 $dt$는 $DT$로 변환되었다.
이제 스위치 OFF 일 때를 구해보자. 포워드 컨버터는 이전의 다른 컨버터들과 비교해볼 때 구조가 조금 복잡한 편이다. 기존에 없던 리셋권선의 동작 메커니즘을 이해해야 하기 때문이다. 스위치가 ON이 되었을 때 인덕터에 에너지가 저장되는데, 스위치가 ON이 되면 인덕터의 전류가 흐를 경로가 없기 때문에 변압기를 통해 자속으로 흐른다. 이 때, 2차측에는 D1에 의해서 전류가 막혀있기 때문에 결국 전류가 흐를 수 있는 경로는 1차측 권선에서 리셋권선 방향 밖에 없다. 이렇게 리셋권선으로 에너지가 전달되면 D3는 순방향 바이어싱되기 때문에 전류가 흐를 수 있고 결과적으로 이 전류가 다시 변압기 쪽으로 흘러서 2차측으로 에너지를 넘겨 코어를 다음 번 동작을 위해서 리셋시킬 수 있다. 자, 이제 아래 수식을 보고 이해해보자.
변압기 관련 내용은 이 글을 참고하자.
$$ v_3 = -V_S $$
$$ v_1 = v_3\frac{N_1}{N_3} = -V_S\frac{N_1}{N_3} $$
$$ v_2 = v_3\frac{N_2}{N_3} = -V_S\frac{N_2}{N_3} $$
$$ v_L = -V_O = L\frac{di_L}{dt} = L\frac{\Delta i_L}{(1 - D)T} $$
$$ \therefore (\Delta{i_L})_{open} = \frac{-V_O(1 - D)T}{L} $$
한 주기 동안의 스위치 OFF 때 인덕터 전류의 변화량
그런데 Rule 6에 의해서 한 주기 동안의 인덕터의 전류는 거의 동일하므로 아래와 같이 입출력 관계식을 얻을 수 있다.
$$ (\Delta{i_L})_{closed} \simeq (\Delta{i_L})_{open} $$
$$ \left [ V_S\frac{N_2}{N_1} - V_O \right ] \frac{DT}{L} - \frac{-V_O(1 - D)T}{L} \simeq 0 $$
$$ V_O \simeq V_SD\frac{N_2}{N_1} $$
포워드 컨버터 입출력 관계식
위 식을 보면, 포워드 컨버터는 벅 컨버터에 턴비가 곱해진 형태라고 볼 수 있다.
위에서 스위치가 ON 일 때 자화 인덕턴스에 흐르는 전류가 선형적으로 올라간다고 얘기했었다. 즉, $\Delta i_{L_m} = \frac{V_SDT}{L_m}$ 인데, 이 자화 인덕턴스에 인가된 에너지가 완전히 리셋되지 않으면 계속해서 자속이 올라가서 자속이 포화되어 버린다. 이렇게 되면 제어가 불가능해지므로, 다음 번 동작을 위해서 인덕턴스의 흐르는 전류는 항상 0이 되도록 해야 한다. 아래의 식을 봐보자.
$$ v_{L_m} = v_1 = V_S\frac{N_1}{N_2} = L_m\frac{di_{L_m}}{dt} $$
$$ \frac{di_{L_m}}{dt} = -\frac{V_S}{L_m}\frac{N_1}{N_2} = \frac{\Delta i_{L_m}}{\Delta t} \tag{1} $$
$$ \frac{V_SDT}{L_m} - \frac{V_S}{L_m}\frac{N_1}{N_2} = 0 \tag{2} $$
$$ \Delta t = DT\frac{N_3}{N_1} $$
변압기 코어 리셋 원리
위에서 (1)식은 스위치가 OFF 일 때 리셋권선에 의한 단위 시간당 변화량을 식으로 나타낸 것이다. (2)식과 같이 스위치가 ON일 때와 스위치가 OFF 일 때가 크기가 같아야 하므로 리셋하기 위해 필요한 최소 시간은 $\Delta t$가 된다. 이로 인해, 포워드 컨버터에는 듀티의 제약(코어 리셋의 의무)가 존재한다. 코어가 리셋되는 시간이 주기보다 짧아야 하는데, 코어가 리셋되는 시간을 $t_0$라고 다음의 식을 봐보자.
$$ t_0 = DT + \Delta t = DT + DT\frac{N_3}{N_1} = DT(1 + \frac{N_3}{N_1}) $$
$$ DT(1 + \frac{N_3}{N_1}) < 1 (\because t_0 < T) $$
듀티 제한
스위치로 사용하고 있는 NMOS에 걸리는 전압에도 유의가 필요하다. NMOS에 드레인에 과도한 전압이 걸리면 고장이 발생할 수 있기 때문이다. (자세한 내용은 MOFSET 고장 시나리오를 참고하자.)
스위치에 걸리는 전압은 이제 $t_0$을 기준으로 표현 가능하다.
$$ v_{sw} = V_S - v_1 = V_S - (-V_S\frac{N_1}{N_3}) = V_S(1 + \frac{N_1}{N_3}) ( for DT < t < t_0 ) $$
$$ v_{sw} = V_S ( for t_0 < t < T ) $$
스위치 전압
위 식을 보면 스위치가 ON 되어 있는 동안 스위치에 더 많은 전압이 인가됨을 알 수 있다.
포워드 컨버터의 2차측은 벅 컨버터와 동일하므로, 커패시턴스와 인덕턴스 크기를 결정하는 로직이 벅 컨버터와 동일하다.
$$ I_{min} = \frac{V_O}{R} - \frac{V_O}{2L}(1 - D)T $$
$$ I_{min} = V_O(\frac{1}{R} - \frac{1}{2L}(1 - D)T) $$
$$ 0 = V_O(\frac{1}{R} - \frac{1}{2L}(1 - D)T) $$
$$ \frac{1}{R} - \frac{1}{2L}(1 - D)T = 0 $$
$$ \therefore L = \frac{(1-D)RT}{2} = \frac{(1-D)R}{2f} $$
인덕터의 전류가 항상 양의 값을 갖도록 하는 최소 인덕턴스 계산
$$ \Delta V_O = \frac{|\Delta Q|}{C} $$
$$ \Delta Q = \frac{1}{2}\frac{T}{2}\frac{\Delta i_L}{2} = \frac{T\Delta i_L}{8} $$
$$ \Delta V_O = \frac{T\Delta i_L}{8C} $$
$$ \Delta V_O = \frac{T^2V_O(1-D)}{8LC} = \frac{V_O(1-D)}{8LCf^2} $$
$$ \frac{\Delta V_O}{V_O} = \frac{(1-D)}{8LCf^2} $$
$$ C = \frac{(1-D)}{8L({\Delta V_O}/{V_O})f^2} $$
출력전압리플 만족을 위한 최소 커패시턴스 계산
리셋을 위한 또 다른 방법 : Active Clamp
Active Clamp 방식을 사용하면 다이오드 방식보다 제어에 있어서 선택권이 넓어질 수 있다. 아래 회로에서는 메인 FET와 클램프 FET의 게이트 신호를 단순히 NOT 게이트를 이용해서 반전한 신호를 입력하도록 했지만 이는 제어 전략에 의해서 변경될 수 있다. 리셋 권선이 2차측으로 자속을 돌려서 자화 인덕터에 흐르는 전류를 0으로 만들어 주는 대신 액티브 클램프 방식은 커패시터에 저장된 에너지가 자화 인덕턴스에 저장된 에너지를 상쇄시키는 방식이라고 볼 수 있다.
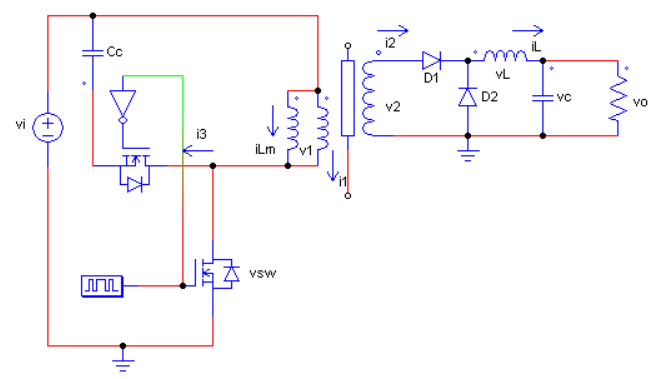

위의 NOT 게이트 방식 대신 PMOS를 사용해서 단순화 시키는 방법도 존재한다(Low Side Active Clamp). 아래의 영상을 참고하자.