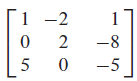선형 독립과 선형 종속
작성일 : 2023년 02월 04일 (Saturday)
Table of contents
선형독립과 선형종속
$$ \mathbb{x}_{1}\mathbb{\textbf{v}}_{1}+ \mathbb{x}_{2}\mathbb{\textbf{v}}_{2}+ \cdot\cdot\cdot+ \mathbb{x}_{n}\mathbb{\textbf{v}}_{n}=\mathbb{\textbf{0}} $$
위 방정식을 만족하는 해가 자명해밖에 없으면 선형 독립이고, 비자명해를 갖는 경우에는 선형 종속이다.
예시
$\mathbb{R}^2$ (2차원)
더 직관적으로 이해하기 위해, 아래의 예시를 보자.

선형독립, 종속 예시 (좌클릭 : 확대 / 우클릭 : 축소)
× 
$$ a : \mathbb{2}\mathbb{\textbf{v}}_{1}=\mathbb{\textbf{v}}_{2} $$
$$ b : c\mathbb{\textbf{v}}_{1} \neq d\mathbb{\textbf{v}}_{2} $$
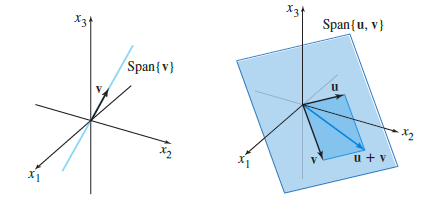
예시 a에서 위와 같이 a는 선형종속이고, 예시 b에서는 두 변수의 관계를 계수를 이용해서 표현할 수 없으므로 선형독립이다. 다른 말로 하면, 어느 벡터의 Span에 포함되는 벡터들끼리는 서로 선형종속관계이고, 같은 Span에 포함되지 않는 벡터들은 서로 선형독립관계이다. 선형종속인 벡터들의 합은 선분까지만 표현할 수 있고, 선형독립인 벡터들의 합은 면까지 표현할 수 있다.
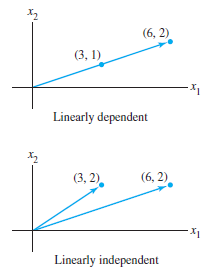
2차원 선형독립, 종속 예시 그래프 (좌클릭 : 확대 / 우클릭 : 축소)
× 
$\mathbb{R}^3$ (3차원)
Span을 이용한 선형독립, 선형종속 판단 방법은 3차원에서도 동일하게 적용된다. 아래 그림을 참고하자.
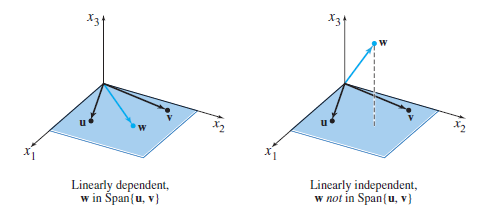
3차원 선형독립, 종속 예시 그래프 (좌클릭 : 확대 / 우클릭 : 축소)
×