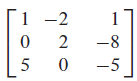행렬대수학과 특성
작성일 : 2023년 02월 04일 (Saturday)
Table of contents
행렬의 곱셈
행렬 곱셈 연산에서는 교환법칙은 일반적으로 성립하지 않는다. 단, 항등행렬(I 혹은 단위행렬)에 대해서는 교환법칙이 성립한다.
곱셈 특성
- $A(BC) = (AB)C$ : 결합법칙
- $A(B + C) = AB + AC$ : 분배법칙
- $(B + C)A = BA + CA$ : 분배법칙
- $\mathbb{r}(AB) = (\mathbb{r}A)B = A(\mathbb{r}B)$ (for any scalar $\mathbb{r}$)
- $I_{m}A = A = AI_{n}$
주의사항
- $AB \neq BA$ (교환법칙 미성립)
- $AB = AC \nRightarrow B = C$
- $AB = 0 \nRightarrow A = \mathbb{\textbf{0}}$ or B = $\mathbb{\textbf{0}}$
전치행렬 (Transpose Matrix)
전치행렬은 행과 열을 서로 바꾼 행렬을 말한다.
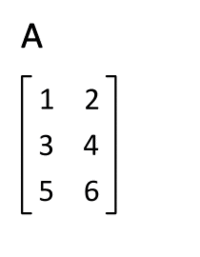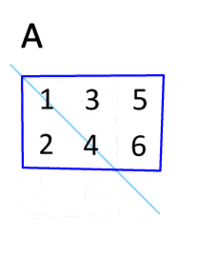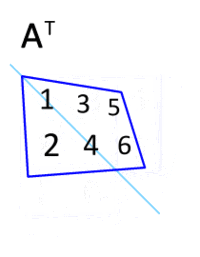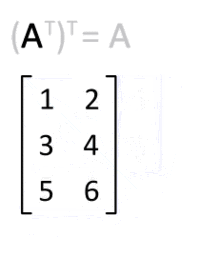

전치행렬에 대해서는 아래의 특성을 만족한다.
- $(A^{T})^{T} = A$
- $(A + B)^{T} = A^{T} + B^{T}$
- $(rA)^{T} = rA^{T}$ (For any scalar $\mathbb{r}$)
- $(AB)^{T} = B^{T}A^{T}$
역행렬 (Inverse Matrix)
역행렬은 원래 행렬에 곱했을 때 결과가 항등행렬이 되게끔 하는 행렬을 말한다. 행렬 $A$가 있을 때, 역행렬은 $A^{-1}$로 표현된다. 위에서 말했다시피 원래 행렬의 곱셈에서는 교환법칙이 성립하지 않지만, 행렬과 역행렬의 곱셈에는 교환법칙이 성립한다. ($AA^{-1} = A^{-1}A = I$)
역행렬은 아래의 같이 계산할 수 있다. (1), (2)가 만족되면 $A$는 역행렬이 존재하고, 그 역행렬은 (3)과 같다. 만약, (2)를 만족하지 못하면 역행렬이 존재하지 않는다. (2)의 ad-bc를 보통 행렬식(determinant)라고 부른다.
$$ \mathbb{\textbf{A}} = \begin{bmatrix}a & b \\ c & d\end{bmatrix} \tag{1} $$
$$ ad-bc \neq 0 \tag{2} $$
$$ A^{-1} = \frac{1}{ad-bc}\begin{bmatrix}d & -b \\ -c & a\end{bmatrix} \tag{3} $$
행렬식의 특성
행렬식은 위에서 설명했듯, 역행렬이 존재하는지 판별할 때 사용된다. 행렬식의 특성은 아래와 같다.
- det $A \neq 0$이면, 역행렬이 존재한다.
- det $AB$ = (det $A$)(det $B$)
- det $A^{T}$ = det $A$
- $A$ 가 삼각행렬$^{*}$이면, det $A$는 $A$의 주 대각선의 곱이다.
- 행연산으로 인해 det $A$가 변하지 않는다. 행의 위치를 서로 바꾸면 det $A$의 부호가 변하고, 행에 특정 값을 곱하면 곱해진 값만큼 det $A$도 변한다.
- 삼각행렬 : 주 대각선의 위나 아래 값이 모두 0인 행렬
역행렬 연산 법칙
- $(A^{-1})^{-1} = A$
- $(AB)^{-1} = B^{-1}A^{-1}$
- $(A^{T})^{-1} = (A^{-1})^{T}$
역행렬 이론
$n$ x $n$ 행렬 A에 대한 아래의 명제들 중 하나라도 만족하면 나머지 명제도 모두 만족한다. 명제의 대우(Proposition)도 성립한다.
- 행렬 $A$는 역행렬이 존재한다.
- 행렬 $A$는 몇 차례의 행연산을 통해서 $n$ x $n$ 항등행렬로 변환할 수 있다. ($n \in \mathbb{N}$)
- $A$는 n개의 추축점을 가진다.
- $A\textbf{x}$ = $\textbf{0}$는 자명해만을 가진다.
- A의 모든 열들은 선형독립이다.
- 선형변환 $\textbf{x} \mapsto A\textbf{x}$는 1:1 관계이다.
- $A\textbf{x}$ = $\textbf{b}$는 $\mathbb{R}^{n}$에 포함된 적어도 하나의 $\textbf{b}$가 존재한다.
- 행렬 $A$의 열들은 $\mathbb{R}^{n}$로 확장된다.
- 선형변환 $\textbf{x} \mapsto A\textbf{x}$은 $\mathbb{R}^{n}$에서 $\mathbb{R}^{n}$에 대한 변환이다.
- $CA = I$ 를 만족시키는 행렬 C가 존재한다.
- $AD = I$ 를 만족시키는 행렬 D가 존재한다.
- $A^{T}$는 역행렬이 존재한다.
- 행렬 $A$의 열들은 $\mathbb{R}^{n}$의 기저이다.
- Col $A$ = $\mathbb{R}^{n}$
- 행렬 A의 열공간의 차원은 n이다.
- rank $A$ = n
- Nul $A$ = {$\textbf{0}$}
- dim Nul $A$ = 0
- 0은 A의 고유값이 될 수 없다.
- A의 행렬식은 0이 아니다.
기본행렬 (Elemental Matrix)
기본행렬은 $I_{n}$(항등행렬)에 한 번의 행 연산으로 얻어지는 행렬을 말한다. 이 기본행렬을 만드는 연산을 기본행연산이라고 한다. 어떤 행렬에 기본행렬을 여러 번 곱하여 단위 행렬로 만들 수 있다면 그 행렬은 가역행렬 또는 역행렬이 존재함을 증명할 수 있고, 기본행연산으로 가역행렬 또는 역행렬을 구할 수 있다.
분할행렬 (Partitioned Matrix)
분할행렬은 원래의 행렬의 특성을 그대로 따른다.
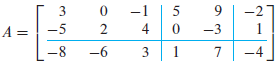
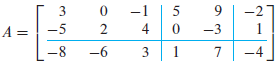
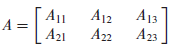
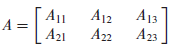
행렬분해 (Matrix Factorization)
행렬을 완전히 합성해놓는 것보다 분해해서 분석하는 것이 분석에 더 용이할 수 있다.