전자기학 기초
작성일 : 2023년 04월 16일 (Sunday)
이번 포스트에서는 직교좌표계를 기준으로 가장 쉬운 형태의 벡터 연산법을 다룬다. 조금 더 일반적인 형태에 대해서 학습하려면 곡면좌표계에서의 연산법을 학습하자.
벡터
선형대수에서도 다뤘던 벡터는 전자기학의 기초가 된다. 벡터의 기본적인 연산에 대해 잘 모르겠다면 벡터 대수학을 복습하자. 전자기학에서는 위치벡터, 변위벡터, 분리벡터의 개념이 사용된다. 벡터는 선속 등을 표현하는데 아주 유용하다.
스칼라장과 벡터장
장이란 무엇일까? 장은 영어로는 Field이다. 물리를 공부할 때 가장 먼저 접하게 되는 중력장을 떠올려보자. 장이란, 어떠한 힘이 작용하는 영역을 말한다. 즉, 어느 Field에 놓이면 그 Field에 의해 에너지를 얻어 운동할 수 있다. 그렇다면 스칼라장과 벡터장이란 무엇일까? 이 질문은 앞으로 전자기학을 공부함에 있어서 모르면 안될 질문이다. 스칼라장이란 특정 영역에서의 특정 값을 갖는 장을 의미한다. 즉, 온도, 압력 등 특정 값으로 측정될 수 있는 값들을 의미한다. 반면에 벡터장은 특정 값을 갖을 뿐만 아니라 방향도 가지고 있다. 즉, 벡터장 내에서 에너지를 얻을 수 있는 있는 대상은 에너지를 얻어 운동하게 된다. 벡터장에는 중력장, 전기장, 자기장 등이 해당된다.
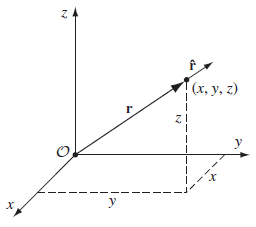
위치벡터 (Position Vector)
원점으로부터 시작하는 벡터를 위치벡터라고 한다.

변위벡터 (Displacement Vector)
변위벡터란 원래 위치에서 이동된 위치를 가리키는 벡터이다. 변위벡터는 두 점 사이를 직선으로 잇는 벡터를 말한다.
분리벡터 (Seperation Vector)
구분벡터는 변위벡터의 일종이다. 구분벡터는 약간의 이동이 있는 위치 벡터(Field Vector)에서 $r’$ 원래의 위치 벡터(Source Vector) $r$를 뺀 벡터를 의미한다.
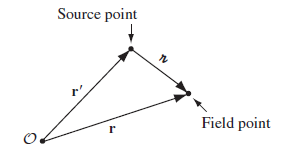

벡터 미적분 연산
벡터를 미적분하면 기하학적으로 더 여러가지 해석이 가능하다. 어느 방 안의 위치 (x, y, z)의 온도를 T(x, y, z)라고 가정하고, 아래를 보자.
Del 연산자 $\nabla $
델 연산자는 아래와 같은 형태이다. 델 연산자에 스칼라 곱, 내적, 외적을 수행하면 각각 경도, 발산, 회전을 구할 수 있다.
$$ \nabla = \frac{\partial }{\partial x}\hat{x} + \frac{\partial }{\partial y}\hat{y} + \frac{\partial }{\partial z}\hat{z} $$
경도 (Gradient) $\nabla T $
dT는 위치 (x, y, z)에서 각 x, y, z 방향에 대한 온도의 미소 변화율을 나타낸다. $\nabla T$는 x, y, z에 대한 단위 온도 변화율을 나타내고 단위 방향 벡터 $\hat{x}$, $\hat{y}$, $\hat{z}$에 각각 변화율을 곱한 값이다.
$$ dT = \frac{\partial T}{\partial x}dx + \frac{\partial T}{\partial y}dy + \frac{\partial T}{\partial z}dz $$
$$ \nabla T = \frac{\partial T}{\partial x}\hat{x} + \frac{\partial T}{\partial y}\hat{y} + \frac{\partial T}{\partial z}\hat{z} $$
경도를 적분하면 경로의 길이를 알 수 있다. (선적분)
선적분 vs 경로적분
선적분과 경로적분은 다르다. 선적분은 스칼라함수 $f : \mathbb{R} ^{n} \rightarrow \mathbb{R} $를 적분하는 것이고, 경로적분은 복소평면에서의 폐경로에 대한 적분을 말한다. (Contour는 윤곽, 테두리라는 의미이고 경로는 지름길을 의미해서 경로적분이라는 우리말 표현이 적합한지는 의문이다..)
선적분은 $\int$를 사용하고, 경로적분은 $\oint$를 사용한다.
경도 정리
$$ dT = (\frac{\partial T}{\partial x}\widehat{x} + \frac{\partial T}{\partial y}\widehat{y} + \frac{\partial T}{\partial z}\widehat{z})(dx \cdot \widehat{x} + dy \cdot \widehat{y} + dz \cdot \widehat{z}) $$
$$ = (\nabla T) \cdot (dl) $$
경도를 이용한 적분
경도를 적분하면 다음과 같이 된다.
$$ \int_{a}^{b} (\nabla T)\cdot dl = T(b) - T(a) $$
발산 (Divergence) $\nabla \cdot T $
발산은 물 웅덩이에 돌맹이를 빠뜨린 경우를 예시로 들어볼 수 있다. 물에 돌맹이를 빠뜨리면 수파가 생겨서 에너지가 0이 될때까지 물이 출렁인다. 파는 아래와 같이 발산된다.
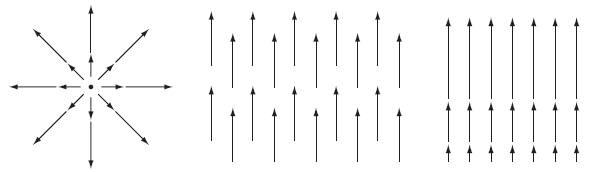

Gradient는 어느 위치에서 에너지가 발산하려는 정도를 나타낸다. 식은 아래와 같다. $T_x$, $T_y$, $T_z$는 (x, y, z) 에서의 에너지 등을 나타낸다.
$$ \nabla \cdot T = \left( \hat{x}\frac{\partial}{\partial x} + \hat{y}\frac{\partial}{\partial y} + \hat{z}\frac{\partial}{\partial z} \right) \cdot (T_x \hat{x} + T_y \hat{y} + T_z \hat{z}) $$
$$ = \frac{\partial T_x}{\partial x} + \frac{\partial T_y}{\partial y} + \frac{\partial T_z}{\partial z} $$
발산 정리
발산을 체적적분하면 다음과 같아진다. 발산 정리는 꽤 중요하다. 가우스 정리, 그린 정리라고도 불리운다.
$$ \int_V (\nabla \cdot v) d\tau = \oint_S v \cdot da $$
내부의 발산을 곡면의 내부에 대해서 모두 적산한 값과 표면에 직각으로 작용하는 벡터의 적산값은 동일하다는 내용이다. 발산정리는 두 벡터의 곱에 대한 발산을 구하려고 할 때 사용될 수 있는데 아래의 예시를 보자.
라플라시안 $\nabla^2 T $
라플라시안 연산자 $\nabla^2 T $는 $\nabla \cdot \nabla T $, 즉 경도의 발산을 말한다. ($\nabla(\nabla \cdot T) $은 라플라시안이 아니기도 하고 실제로 사용할 곳이 없는 연산이니 주의가 필요하다.) 경우에 따라 $\nabla^2$ 대신 $\Delta$가 쓰이기도 한다.
경도의 발산이라는 것이 바로 와닿지 않는 것이 사실이다. 속도는 에너지와 관계가 있으므로, 경도의 발산이 0이 된다는 것은 특정 곡면에 대해서 에너지가 발산되거나 흡수되지 않는 상태를 말한다.
더 쉽게 설명하기 위해 어느 물체가 한 방향으로 직선 운동하는 경우를 예시로 들어보겠다. 변위를 적분하면 속도가 되고, 속도를 적분하면 가속도가 된다. 경도는 1차 미분, 라플라시안은 2차 미분이라고 생각하면 된다. 즉, 라플라시안이 0이 되는 지점은 가속도가 0이 되는 지점을 말한다. 고등학생 때 지겹도록 보던 2차 방정식과 1차 도함수, 2차 도함수와 동일하다.
$$ \nabla ^2 t = \frac{\partial ^2 t}{\partial x^2} + \frac{\partial ^2 t}{\partial y^2} + \frac{\partial ^2 t}{\partial z^2} $$
그림, 영상 등에서 윤곽을 포착하는 데 사용하기도 한다. 라플라시안이 상태(경향)가 변하는 곳을 찾아내는데 쓰일 수 있다는 점을 고려하면 특별히 놀라운 일은 아니다.
회전 (Curl) $\nabla \times T $
회전은 특정 위치에서의 회전의 방향과 힘의 크기를 계산할 때 사용된다. 쉬운 예시를 들어 설명하면, 자기장이 있는 무한한 공간이 있다고 가정했을 때 그 곳에 철이 떨어졌을 때 어느 방향으로 회전할지 구할 때 회전(curl)을 사용할 수 있다.
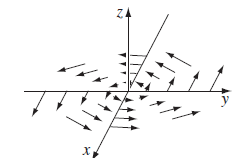

Curl 계산식은 아래와 같다.
$$ \nabla \times v = \begin{bmatrix}\hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ T_x & T_y & T_z \end{bmatrix} $$
$$ = \hat{x}\left( \frac{\partial T_z}{\partial y} - \frac{\partial T_y}{\partial z} \right) + \hat{y}\left( \frac{\partial T_x}{\partial z} - \frac{\partial T_z}{\partial x} \right) + \hat{z}\left( \frac{\partial T_y}{\partial x} - \frac{\partial T_x}{\partial y} \right) $$
$$ = \hat{x}\left( \frac{\partial T_z}{\partial y} - \frac{\partial T_y}{\partial z} \right) - \hat{y}\left( \frac{\partial T_z}{\partial x} - \frac{\partial T_x}{\partial z} \right) + \hat{z}\left( \frac{\partial T_y}{\partial x} - \frac{\partial T_x}{\partial y} \right) $$
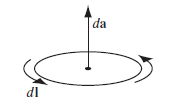
스토크 정리
회전의 면적분은 다음과 같이 정리된다.
$$ \int_S (\nabla \times v)\cdot da = \oint_P v \cdot dl $$
스토크 정리는 아래 그림으로 정리된다. 간단히 말하면 면적분을 수행했을 때 경계를 제외한 내부에서의 회전값들은 서로 상쇄되어 폐경로에 대해서만 그 값이 유효하다는 의미이다.
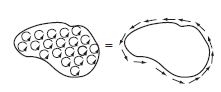


회전의 발산 $\nabla \cdot (\nabla \times T) $
회전의 발산은 항상 0이다. 왜냐하면, 발산은 뚫고 나가는 선속을 더하는 것인데 회전은 원심력 등 벡터의 회전과 관련된 값이어서 발산과 90도를 이루기 때문이다. 결과적으로 내적은 90도일 때 0이므로 회전의 발산은 0이 된다.
경도의 회전 $\nabla \times (\nabla T) $
경도의 회전 역시 항상 0이다. 그라디언트를 $T_x$, $T_y$, $T_z$에 대입하고 값을 구하면 0이 나와서 모두 지워져서 0이 된다. 생각해보면 폐곡면, 폐곡선에 대해서 그라디언트를 구해서 모두 더하면 0이 된다는 것을 직감적으로 알 수 있기도 하다.
첨언
발산의 경도, 회전의 회전은 사실 쓸 일이 없다. 위에서 다룬 내용 정도만 이해하고 있자.