푸리에 변환 (연속 시간)

작성일 : 2023년 03월 05일 (Sunday)

Table of contents

푸리에 변환
1. 푸리에 변환의 수렴

푸리에 변환

푸리에 변환은 푸리에 시리즈에서 주기를 무한대로 늘리면 비주기함수에도 적용가능하다는 아이디어에서 기인했다. 푸리에 변환은 주파수 관련 해석 작업(시스템 디자인)에서 많이 사용된다 (예시). 푸리에 변환은 비주기함수(수렴 조건을 만족하는 함수에 한함)를 주파수 스펙트럼으로 변환하는데 사용하고, 푸리에 역변환은 주파수 스펙트럼을 다시 원래의 함수로 복원하는데 사용한다.

아래는 맨 마지막에 첨부된 이 글을 쓰는데 큰 도움이 된 영상 중 일부를 발췌한 gif이다. 푸리에 변환은 함수 $f(t)$에 $e^{-jwt}$를 곱하고 그 값을 모든 시간에 대해서 적분한 형태인데, $e^{-jwt}$가 사용되는 이유는 영상에서도 나오지만 회전과 감기를 설명하는데 유용하기 때문이다. 부호 -는 회전을 시계방향으로 하기 위함이다. 푸리에 변환은 시계방향으로 감아서 주파수 스펙트럼을 분석하는데 사용하고, 푸리에 역변환은 주파수 스펙트럼을 반시계방향으로 다시 되감아 원래의 신호를 얻어내는 작업이다.

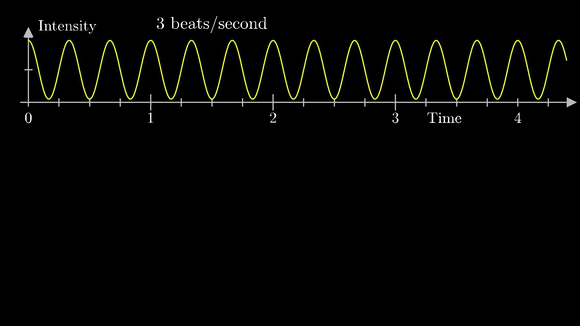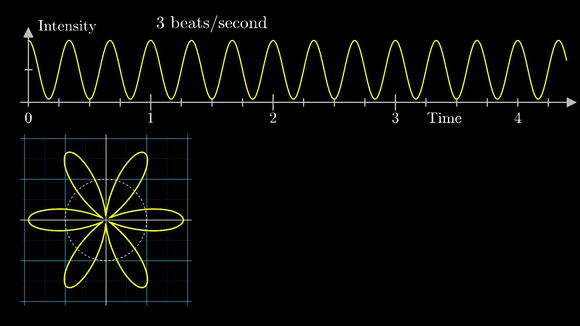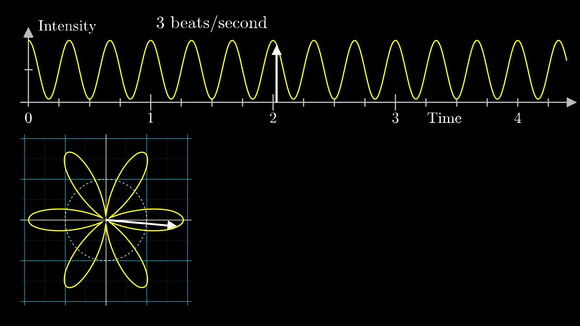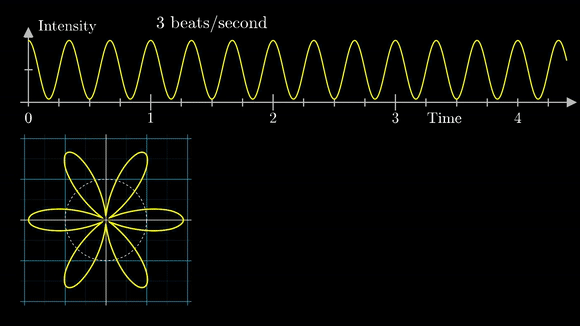
이제 수식으로 풀어보자. 다시, 푸리에 시리즈식을 상기해보자.

$$ f(t)=\sum_{k=-\infty}^{\infty}c_k\exp\left(j \frac{2\pi k t}{T}\right) $$

$$ c_k = \frac{1}{T}\int_{0}^{T}f(t)\exp\left(-j\frac{2\pi k t}{T}\right)dt = \frac{1}{T}\int_{-T/2}^{T/2}{f(t) \exp \left(-j \frac{2\pi k}{T}t\right)dt} $$

푸리에 시리즈 요약

T를 $\infty$로 보내면, 비주기함수에도 푸리에 시리즈를 사용할 수 있다고 말했다. 위 푸리에 시리즈에서 $f(t)$에 $c_{k}$식을 넣고 양변에 T를 양의 무한대로 보내는 리미트를 취하여 정리하면 푸리에 역변환식이 구해진다.

$$ \lim_{T\rightarrow \infty}f(t)= \lim_{T\rightarrow\infty} \sum_{k=-\infty}^{\infty}\left[\frac{1}{T}\int_{-T/2}^{T/2}{f(t) \exp\left(-j \frac{2\pi k}{T}t\right)dt}\right]exp\left(j\frac{2\pi k}{T}t\right) $$

$$ = \sum_{k=-\infty}^{\infty} \lim_{T\rightarrow\infty} \left[ \int_{-T/2}^{T/2}{f(t) \exp\left(-j \frac{2\pi k}{T}t\right)dt}\right] \exp\left(j\frac{2\pi k}{T}t\right) \frac{1}{T} $$

$$ \therefore f(t) = \int_{-\infty}^{\infty} F(f) exp\left(j2\pi ft\right)df $$

푸리에 역변환 식 유도

T가 무한대로 보내지면 k/T는 결국에는 연속적인 주파수로 볼 수 있다. 위 역변환 식 과정 중 부족한 내용은 다음을 참고하자.

$$ \sum_{k=-\infty}^{\infty} \lim_{T\rightarrow\infty} \int_{-T/2}^{T/2} \left[ \frac{k}{T} \right] \cdot \frac{1}{T} $$

$$ = \sum_{k=-\infty}^{\infty} \lim_{T\rightarrow\infty} \int_{-\infty}^{\infty} \left[ \frac{k}{T} \right] \cdot \frac{1}{T} $$

$$ = \int_{-\infty}^{\infty} f df $$

결과적으로, 정리하면 아래와 같다.

$$ F(f) = \int_{-\infty}^{\infty}f(t) \exp\left(-j2\pi ft\right)dt $$

푸리에 변환 식

$$ f(t) = \int_{-\infty}^{\infty} F(f) exp\left(j2\pi ft\right)df $$

$$ = \frac{1}{2\pi}\int_{-\infty}^{\infty} F(w) exp\left(jwt\right)dw $$

푸리에 역변환 식

푸리에 변환식과 역변환식을 보면, $t$대신 $-f$를 대입하면 변환식에서 역변환식이 얻어지고, 반대로 역변환식에서 변환식이 얻어진다. 이러한 특성을 쌍대성(Duality)이라고 하는데, 이 쌍대성에 의해서 $f(t) \Leftrightarrow F(f)$ 간 변환이 용이하다. 예를 들어서, 임펄스함수 $\delta ({t})$를 푸리에 변환하면 1이 된다. 반대로 $\delta ({f})$를 푸리에 역변환하면 1이 얻어진다. 이미 만들어진 푸리에 변환/역변환표를 사용하면 보다 간편하게 푸리에 변환/역변환을 수행할 수 있다.

푸리에 변환의 수렴

비주기함수를 푸리에 변환으로 정현파의 합으로 표현했을 때 그 변환이 유효하려면 수렴조건을 만족해야 한다. 여기서 수렴이란, 변환된 함수가 원래함수와 거의 동일해지는 특성을 말한다. 즉, 수렴하지 않으면 푸리에 변환은 존재하지 않는다고 생각할 수 있다. 수렴조건은 푸리에 시리즈와 동일하다. (디리클레 조건)