푸리에 시리즈 (이산 시간)
작성일 : 2025년 05월 11일 (Sunday)
Table of contents
이산시간 푸리에 시리즈 DTFS도 CTFS 와 동일하게 주기함수에 대해서 사용할 수 있다. DTFS 역시 한 주기 <N>만을 합산한다. DTFS는 \(e^{jk\varOmega n}\) 을 기저함수로 한다. 기저함수에 대해서는 CTFS를 참고한다.
식
DTFS(Disrete Time Fourier Series)식은 아래와 같다. <N>이 의미하는 바는 한 주기의 데이터를 반영하라는 의미이다. <N>은 보통 0~N-1로 사용된다. \(\frac{2\pi}{N}\) 은 흔히 기본 각주파수 \(\varOmega_{0}\) 로도 표현된다.
$$ a_{k} = \frac{1}{N}\sum_{n=\left\langle N \right\rangle }\widetilde{x}[n] e^{-j \frac{2\pi k}{N}n} \text{ for }k= 0, 1, \cdots, N-1 $$
Analysis Eqution (DTFS)
$$ \widetilde{x}[n] = \sum_{k=\left\langle N \right\rangle }a_{k} e^{j\frac{2\pi k}{N}n} = \sum_{k=\left\langle N \right\rangle }a_{k} e^{j\varOmega_{0}kn} $$
Synthesis Eqution (DTFS)
앨리어싱 방지
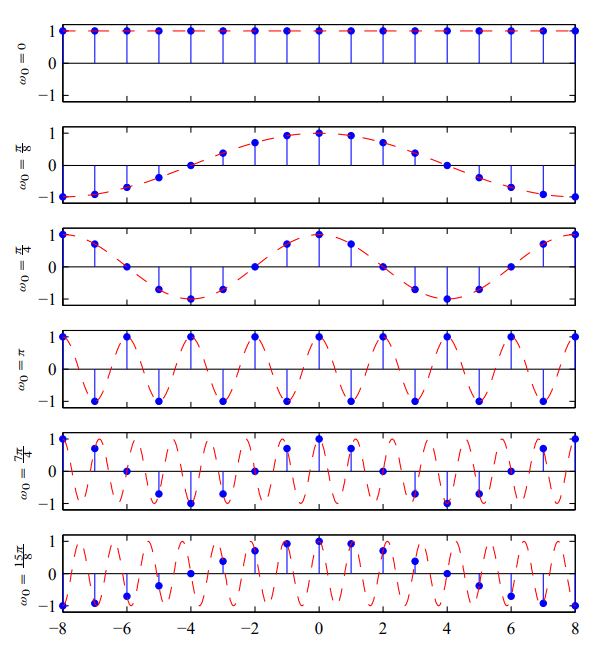
앨리어싱을 방지하기 위해서 샘플링 주파수가 최소 최대주파수의 2배 이상이 되도록 설정해주어야 한다. 아래의 그림을 봐보자. 같은 샘플링 시간으로 샘플링했을 때 \(w_{0} = \frac{7 \pi}{4}\) 부터 원신호로 복원되지 않을 수 있다는 것을 직접 확인할 수 있다.

푸리에 시리즈에서 복소정현파를 사용하는 이유
푸리에 시리즈에서 복소정현파를 사용하는 이유에 대해서는 이전 연속시간 푸리에 시리즈 포스트에서 다뤘다. 이유는 동일하다.
이산시간에서의 내적은 아래와 같이 표현한다.
$$ \sum_{n=0}^{N-1}{\phi_k[n]\phi^*_p[n] =0 \text{ when } k\neq p } $$
DTFS 특성
$$ \widetilde{x_1}[n] \leftrightarrow \widetilde{X_1}[k] $$
$$ \widetilde{x_2}[n] \leftrightarrow \widetilde{X_2}[k] $$
$$ a_1\widetilde{x_1}[n] + a_2\widetilde{x_2}[n] \leftrightarrow a_1\widetilde{X_1}[k] + a_2\widetilde{X_2}[k] $$
Linearity
$$ \widetilde{x_1}[n]\widetilde{x_2}[n] \leftrightarrow \sum_{n=0}^{N-1}\widetilde{X_1}[k]\widetilde{X_2}[k - n] $$
$$ \widetilde{X_1}[k]\widetilde{X_2}[k] \leftrightarrow \sum_{n=0}^{N-1}\widetilde{x_1}[m]\widetilde{x_2}[n - m] $$
Convolution & Duality