라플라스 변환
작성일 : 2023년 03월 12일 (Sunday)
Table of contents
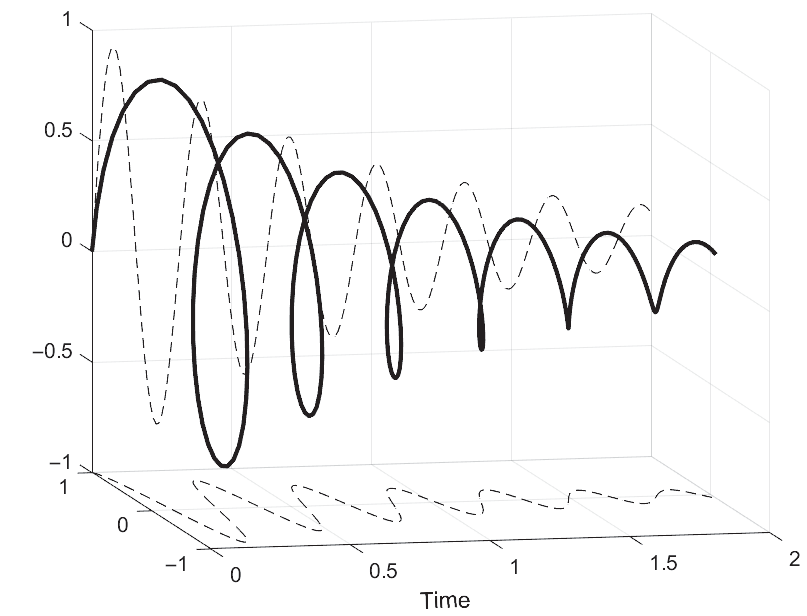
라플라스 변환은 푸리에 변환의 한계점을 극복한 변환이다. 푸리에 변환은 디리클레 조건에 의해서 모든 구간에 대해 완전히 적분가능해야 해서 발산하는 신호에 대해서는 적용이 불가능했었다. 라플라스 변환의 핵심 개념은 감쇄되는 신호인 $e^{-\sigma t}$를 커널함수로 이용해서 어느 정도 발산하는 신호에 대해서도 발산을 억제하여 변환이 가능하도록 하는 것이다. 푸리에 변환보다 완화된 수렴 조건만 만족하면, 발산하는 신호에 대해서도 적용할 수 있기 때문에 조금 더 일반적으로 사용된다. 정리하자면, 푸리에 변환은 라플라스 변환의 가장 간단한 버전($\sigma = 0$)이라고 할 수 있다.
Unilateral(One-Sided) Laplace Transform (단방향 라플라스 변환)
단방향 라플라스 변환은 초기조건이 없는 경우에 사용된다. 즉, LTI 시스템이라면 Causality 특성에 의해서 양방향 라플라스 변환을 사용해야 한다.
$$ F(s) = \mathcal{L}[f(t)] = \int_{0^{-}}^{\infty}f(t)e^{-st}dt $$
$$ (0^{-} = \lim{\epsilon \to 0}{0 - \epsilon}) $$
$$ s = \sigma + jw $$
단방향 라플라스 변환 (Unilateral(One-Sided) Laplace Transform)
Bilateral(Two-Sided) Laplace Transform (양방향 라플라스 변환)
양방향 라플라스 변환은 초기조건이 0이 아닌 경우, 이전 입력값까지 포함하여 분석하기 위한 변환이다. 양방향 라플라스 변환은 $\mathcal{L}$대신 $\mathcal{B}$로도 표현한다.
$$ F(s) = \mathcal{B}[f(t)] = \int_{-\infty}^{\infty}f(t)e^{-st}dt $$
$$ s = \sigma + jw $$
양방향 라플라스 변환 (Bilateral(Two-Sided) Laplace Transform)
라플라스 변환의 수렴 조건 (ROC; Region of Convergence)
라플라스 역변환
$\gamma$는 경로적분이 F(s)의 ROC안에 있도록 하는 값이다.
$$ f(t) = \mathcal{L}^{-1}\{ F \}(t) = \frac{1}{2\pi i}\lim_{T \rightarrow \infty}\int_{\gamma -iT}^{\gamma + iT}F(s)e^{st}ds $$
라플라스 역변환
라플라스 변환의 의의
- 참고문헌
- Daniel Fleisch - A Student’s Guide to Laplace Transforms-Cambridge University Press (2022)
