영점 및 극점 추가 효과
작성일 : 2023년 01월 25일 (Wednesday)
Table of contents
전달함수의 영점과 극점
전달함수의 영점과 극점은 시스템의 특성을 해석/설계하는 데 있어서 중요한 요소이다. 영점과 극점이 추가됨에 따라서 시스템의 특성이 변화된다. 영점이란 전달함수를 0으로 가게끔 분자를 구성하는 함수가 0이 되게끔 하는 값이고, 극점은 전달함수의 분모함수가 0이 되게끔 하는 값들을 말한다.
영점 추가 효과
아래와 같이 $1+T_zs$을 곱해서 $s=-\frac{1}{T_z}$에 영점을 추가한 케이스를 고려해보자. $T_z$를 변화시키면 아래와 같이 파형의 진폭이 변화된다.
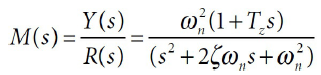
(좌클릭 : 확대 / 우클릭 : 축소)
× 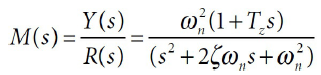

(좌클릭 : 확대 / 우클릭 : 축소)
× 
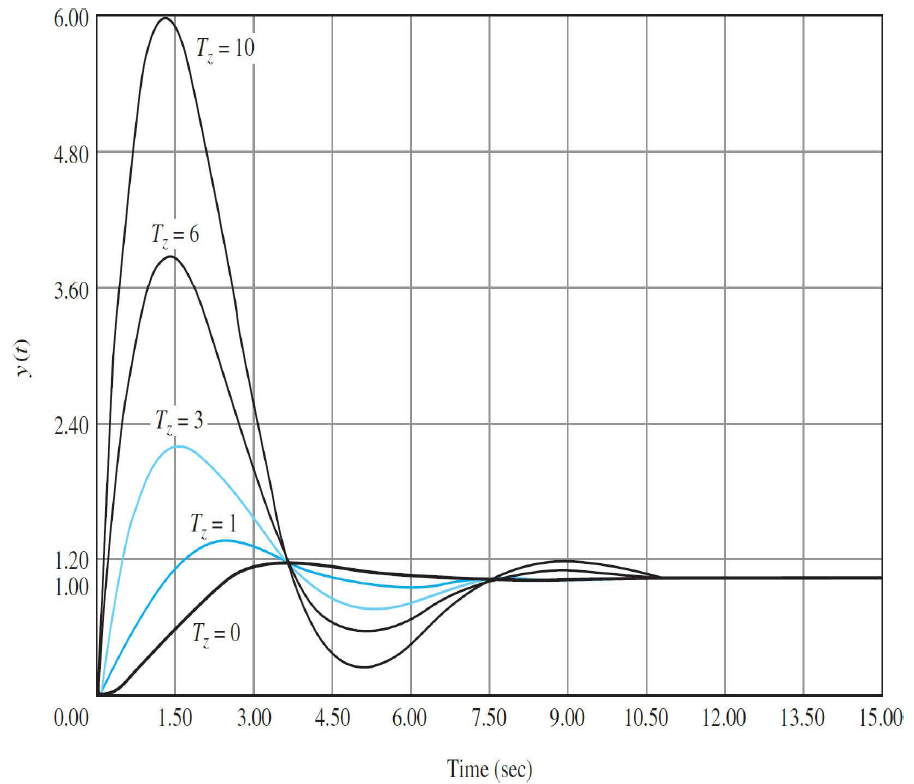
영점 추가에 따른 그래프 변화 (좌클릭 : 확대 / 우클릭 : 축소)
× 
극점 추가 효과
아래와 같이 개방 루프 이득 함수에 극점을 추가한 케이스를 고려해보자.
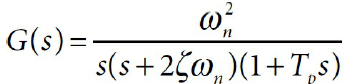
개루프 이득 (좌클릭 : 확대 / 우클릭 : 축소)
× 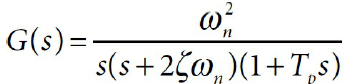
만약 피드백 이득이 1이라고 가정하면, 폐루프 이득은 아래와 같다.
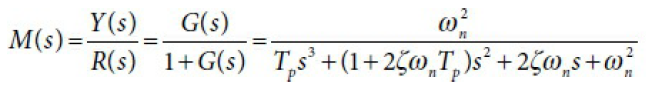
폐루프 이득 (좌클릭 : 확대 / 우클릭 : 축소)
× 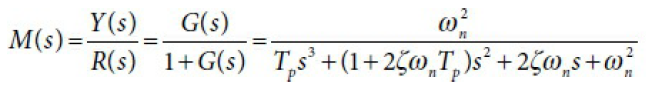
$T_p$를 변화시키면 아래와 같이 정착시간, 지연시간, 상승시간 등이 변경된다.

극점 추가에 따른 극점 변화 (좌클릭 : 확대 / 우클릭 : 축소)
× 
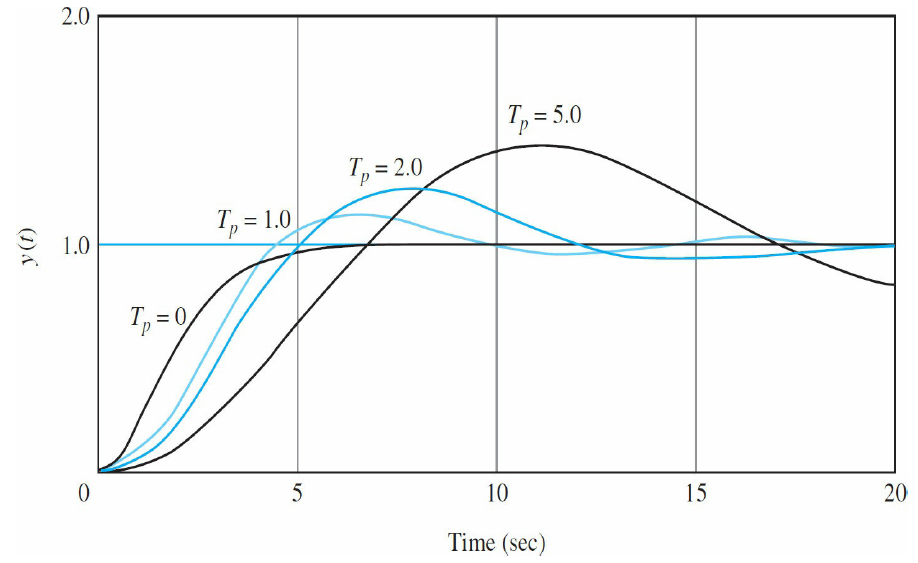
극점 위치에 따른 그래프 (좌클릭 : 확대 / 우클릭 : 축소)
× 
우세극점 (Dominant pole)
극점을 추가하더라도 그 극점이 우세극점이 아니라면 시스템에 미치는 정도가 아주 미미하다. 그렇다면 무엇이 우세극점이고 무엇이 구별할 수 있어야 한다.
우세극점
시스템마다 정확한 위치는 다르지만 우세극점과 우세극점이 아닌 극점들이 위치한 영역은 아래와 같이 영역으로 구분한다. 정확한 위치와 형태는 시스템에 따라 달라진다.
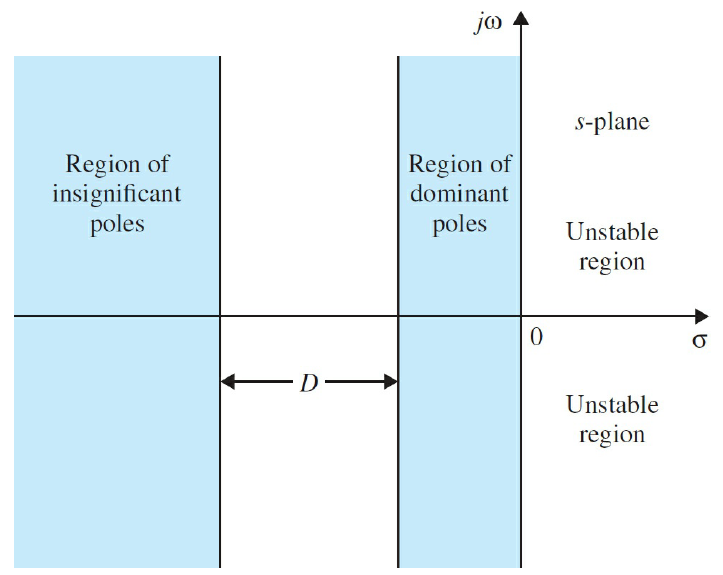
우세극점의 일반적인 영역 (좌클릭 : 확대 / 우클릭 : 축소)
× 
감쇠비 등을 고려하면 아래와 같이 영역이 설정되기도 한다.
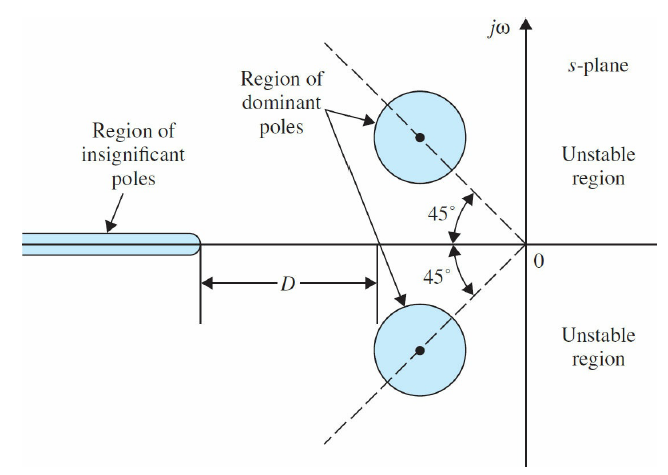
감쇠비를 고려한 우세극점 영역 (좌클릭 : 확대 / 우클릭 : 축소)
×